【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
参考答案:
【答案】(1)8,7.5 ;(2)乙运动员的射击成绩更稳定.
【解析】
试题分析:(1)求甲的平均数只要把甲的十次射击成绩加在一起除以10即可;求乙的中位数先把乙的十次射击成绩按从小到大顺序排列,则排在中间两个数据的平均数就是乙的中位数;(2)先计算出甲,乙的平均数,根据方差计算公式(各个数据与平均数差的平方和再除以10),即可算出两位运动员的方差,谁的方差小,谁的成绩就稳定.
试题解析:(1)把甲的十次射击成绩加在一起除以10:甲的平均数=(6+10+8+9+8+7+8+10+7+7)÷10=8;先把乙的十次射击成绩按从小到大顺序排列为7,7,7,7,7,8,9,9,9,10.则排在中间两个数据是7,8.故乙的中位数是(7+8)÷2=7.5;(2)甲的平均数是8,乙的平均数是(7+7+7+7+7+8+9+9+9+10)÷10=8,故![]()
![]() ,
,![]() =
=![]() ,
,![]() ,∴乙运动员的射击成绩更稳定.
,∴乙运动员的射击成绩更稳定.
-
科目: 来源: 题型:
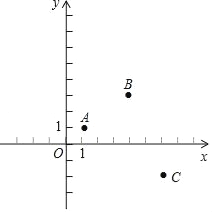
查看答案和解析>>【题目】已知A(1,1),B(4,3),C(6,﹣2),在平面直角坐标找一点D,使以A、B、C、D四点的四边形为平行四边形,则D点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的对称轴为经过点(1,0)的直线,其图象与x轴交于点A、B,且过点C(0,﹣3),其顶点为D.
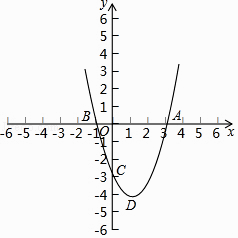
(1)求这个二次函数的解析式及顶点坐标;
(2)在y轴上找一点P(点P与点C不重合),使得∠APD=90°,求点P的坐标;
(3)在(2)的条件下,将△APD沿直线AD翻折得到△AQD,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图1所示).探究 如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.
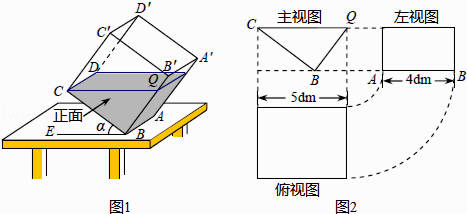
解决问题:
(1)CQ与BE的位置关系是 , BQ的长是dm;
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积S△BCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°= ,tan37°=
,tan37°=  )
)
(4)延伸:在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM=1dm,BM=CM,NM⊥BC.继续向右缓慢旋转,当α=60°时,通过计算,判断溢出容器的液体能否达到4dm3 .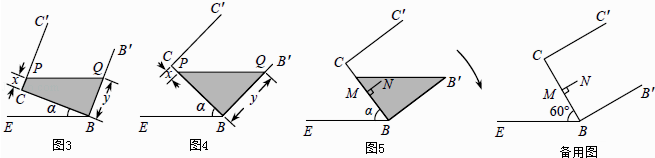
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣
 )=0.
)=0.(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为( )
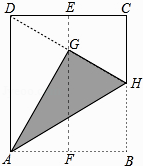
A.2cm
B.2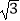 cm
cm
C.4cm
D.4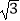 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的周长为 .

相关试题

