【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D, BE⊥MN于E.
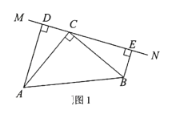
(1)当直线MN绕点C旋转到图1的位置时,求证:△ADC≌△CEB;
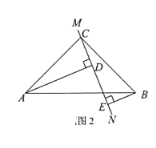
(2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE的等量关系?并说明理由.
参考答案:
【答案】(1)见解析;(2)DE=AD-BE,理由见解析
【解析】
(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;
(2)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,即可得到答案.
解:(1)证明:如图1,
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
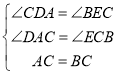 ,
,
∴△ADC≌△CEB(AAS);
(2)结论:DE=AD-BE.
理由:如图2,∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
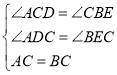 ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC-CD=AD-BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
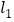 :y=2x+1与直线
:y=2x+1与直线 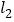 :y=mx+4相交于点P(1,b)
:y=mx+4相交于点P(1,b)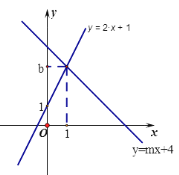
(1)求b,m的值
(2)垂直于x轴的直线 x=a与直线
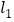 ,
,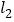 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解答过程,然后再解题.
例:已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x 2+ax+b),
则2x 3﹣x2+m=2x 3+(2a+1)x2+(a+2b)x+b.
比较系数得
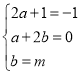 ,解得
,解得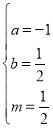 ,∴m=
,∴m=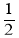 .
.解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取x=﹣
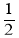 ,2×(﹣)3﹣(﹣)2+m=0,故m=
,2×(﹣)3﹣(﹣)2+m=0,故m=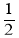 .
.(1)已知多项式2x3﹣2x2+ m有一个因式是x+2,求m的值.
(2)已知x 4+ m x3+ n x﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=45°.若AD平分∠BAC交BC于D,BE⊥AC于E,且交A于O,连接OC.则下列说法中正确的是( )①AD⊥BC;②OC平分BE;③OE=CE;④△ACD≌△BCE;⑤△OCE的周长=AC的长度
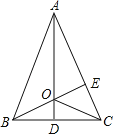
A.①②③B.②④⑤C.①③⑤D.①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
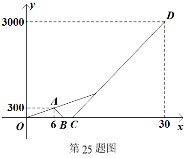
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
⑴小亮在家停留了 分钟.
⑵求小亮骑单车从家出发去图书馆时距家的路程y(米)与出发时间x(分钟)之间的函数关系式.
⑶若小亮和姐姐到图书馆的实际时间为m分钟,原计划步行到达图书馆的时间为n分钟,则n-m= 分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一架方梯AB长25米,如图所示,斜靠在一面上:

(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
相关试题

