【题目】某商店销售甲、乙两种商品,现有如下信息: 请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)
参考答案:
【答案】
(1)解:设甲商品进货单价x元,乙商品进货单价y元.
依题意,得
![]()
解得: ![]() .
.
答:甲商品进货单价为1元,乙商品进货单价为2元
(2)解:依题意,得
(2﹣m﹣1)(500+1000m)+(3﹣2)×1300=1800
(1﹣m)(500+1000m)=500
即2m2﹣m=0
∴m1=0.5,m2=0
∵m>0
∴m=0不合舍去,即m=0.5
答:当m=0.5时,商店获取的总利润为1800元
【解析】(1)根据图上信息可以得出甲乙商品之间价格之间的等量关系,即可得出方程组求出即可;(2)根据降价后甲每天卖出:(500+ ![]() ×100)件,每件降价后每件利润为:(1﹣m)元;即可得出总利润,利用一元二次方程解法求出即可.
×100)件,每件降价后每件利润为:(1﹣m)元;即可得出总利润,利用一元二次方程解法求出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;…,学生发现这些勾股 数的勾都是奇数,且从 3 起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、________、________;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示?小明发现每组第二个数有这样的规律4=
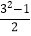 ,12=
,12=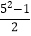 ,24=
,24=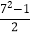 ……,于是他很快表示了第二数为
……,于是他很快表示了第二数为  ,则用含a的代数式表示第三个数为________;
,则用含a的代数式表示第三个数为________;(3)用所学知识证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为y(米)与时间x(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:a=________;b=________;m=________.
(2)若小军的速度是 120 米/分,求小军第二次与爸爸相遇时距图书馆的距离.
(3)在(2)的条件下,爸爸自第二次出发后,骑行一段时间后与小军相距100 米,此时 小军骑行的时间为________分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



-
科目: 来源: 题型:
查看答案和解析>>【题目】一副直角三角板如图放置,点A在ED上,∠F=∠ACB=90°,∠E=30°,∠B=45°,AC=12,试求BD的长.
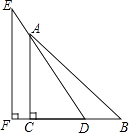
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
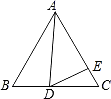
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
相关试题

