搜索
【题目】在平面直角坐标系中，点A（1，1），B（4，3），将点A向左平移2个单位长度，再向上平移3个单位长度得到点C．
（1）写出点C的坐标；
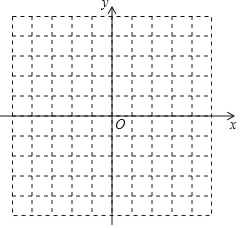
（2）画出△ABC并判断△ABC的形状．
参考答案：
【答案】（1）C（﹣1，4）；（2）△ABC是等腰直角三角形；过程见详解.
【解析】
（1）根据向左平移2个单位长度为横坐标减2，向上平移3个单位长度为纵坐标加3，即可得到C点坐标.
（2）如图，顺次连接A，B，C，然后根据每个点的坐标利用两点间的距离公式分别求出AB，BC，CA的长，再根据勾股定理逆定理判断即可.
（1）∵将点A（1，1）向左平移2个单位长度，再向上平移3个单位长度得到点C，
∴C（﹣1，4）；
（2）△ABC是等腰直角三角形；
如图所示，根据勾股定理得，AB=
=
=
，
BC=
=
=
，
AC=
=
=，
∴AB=AC，
∵AB2+AC2=BC2=26，
∴△ABC是直角三角形，
∴△ABC是等腰直角三角形．
-
科目： 来源： 题型：
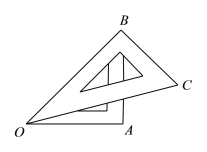
查看答案和解析>>【题目】如图，将一幅三角板摆放在一起．
（1）∠AOC的度数为________，射线OA 、OB、OC组成所有小于平角的和为________；
（2）反向延长射线OA 到D，OE为∠BOD的平分线，OF为∠COD的平分线，请按题意画出图形，并求出∠EOF的度数．
-
科目： 来源： 题型：
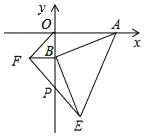
查看答案和解析>>【题目】如图，点A的坐标为（4，0），点B从原点出发，沿y轴负方向以每秒1个单位长度的速度运动，分别以OB，AB为直角边在第三、第四象限作等腰Rt△OBE，等腰Rt△ABF，连结EF交y轴于P点，当点B在y轴上运动时，经过t秒时，点E的坐标是_____（用含t的代数式表示），PB的长是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx经过A（4，0），B（1，3）两点，点B、C关于抛物线的对称轴l对称，过点B作直线BH⊥x轴，交x轴于点H．
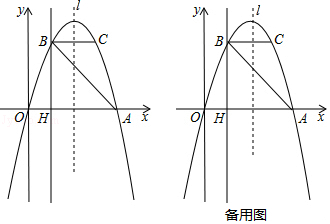
（1）求抛物线的解析式；
（2）若点M在直线BH上运动，点N在x轴上运动，是否存在这样的点M、N，使得以点M为直角顶点的△CNM是等腰直角三角形？若存在，请求出点M、N的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，长方形OABC的边OC=2，将过点B的直线y=x﹣3与x轴交于点E．
（1）求点B的坐标；
（2）连结CE，求线段CE的长；
（3）若点P在线段CB上且OP=
，求P点坐标．
-
科目： 来源： 题型：
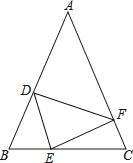
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，点D，E，F分别在AB，BC，AC边上，且BE=CF，BD=CE．
（1）求证：△DEF是等腰三角形；
（2）当∠A=50°时，求∠DEF的度数；
（3）若∠A=∠DEF，判断△DEF是否为等腰直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
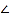AOC=
，ON是锐角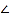COD的角平分线，OM是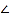AOC的角平分线，那么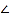，MON= （ ）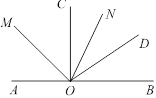
A.
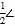COD+
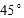B. C.
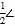AOD D.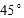
相关试题
