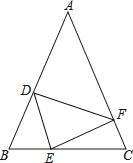
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等腰直角三角形.
参考答案:
【答案】(1)见解析;(2)∠DEF=65°;(3)△DEF不可能是等腰直角三角形.
【解析】
(1)根据AB=AC可得∠B=∠C,再利用“边角边”得到△BDE≌△CEF,即可得证;
(2)根据(1)中得到的全等三角形可得∠CEF=∠BDE,于是得到∠DEF=∠B,再根据等腰三角形的性质即可得解;
(3)由(1)知:△DEF是等腰三角形,即DE=EF,由(2)知,∠DEF=∠B,所以△DEF不可能为等腰直角三角形.
解:(1)∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
∵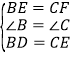 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B,
又∵在△ABC中,AB=AC,∠A=50°,
∴∠B=65°,
∴∠DEF=65°;
(3)由(1)知:△DEF是等腰三角形,即DE=EF,
由(2)知,∠DEF=∠B,
而∠B不可能为直角,
∴△DEF不可能是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx经过A(4,0),B(1,3)两点,点B、C关于抛物线的对称轴l对称,过点B作直线BH⊥x轴,交x轴于点H.
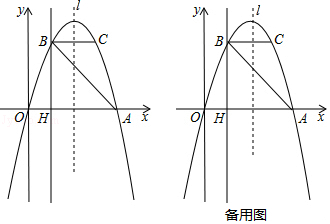
(1)求抛物线的解析式;
(2)若点M在直线BH上运动,点N在x轴上运动,是否存在这样的点M、N,使得以点M为直角顶点的△CNM是等腰直角三角形?若存在,请求出点M、N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(1,1),B(4,3),将点A向左平移2个单位长度,再向上平移3个单位长度得到点C.
(1)写出点C的坐标;
(2)画出△ABC并判断△ABC的形状.
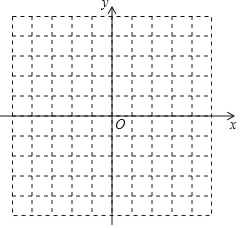
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形OABC的边OC=2,将过点B的直线y=x﹣3与x轴交于点E.
(1)求点B的坐标;
(2)连结CE,求线段CE的长;
(3)若点P在线段CB上且OP=
 ,求P点坐标.
,求P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
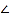 AOC=
AOC= ,ON是锐角
,ON是锐角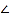 COD的角平分线,OM是
COD的角平分线,OM是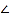 AOC的角平分线,那么,
AOC的角平分线,那么,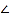 MON= ( )
MON= ( )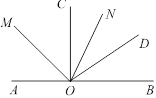
A.
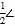 COD+
COD+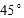 B.
B. 
C.
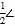 AOD D.
AOD D. 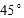
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形有一组对角互补(即对角之和为180°),则称这个四边形为圆满四边形.
(1)概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于圆满四边形的有 .
(2)问题探究:如图,在四边形ABCD中,对角线AC、BD相交于点O,若∠ADB=∠ACB,问四边形ABCD是圆满四边形吗?请说明理由.小明经过思考后,判断四边形ABCD是圆满四边形,并提出了如下探究思路:先证明△AOD∽△BOC,得到比例式 =
= 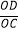 ,再证明△AOB∽△DOC,得出对应角相等,根据四边形内角和定理,得出一组对角互补.请你帮助小明写出解题过程.
,再证明△AOB∽△DOC,得出对应角相等,根据四边形内角和定理,得出一组对角互补.请你帮助小明写出解题过程.
(3)问题解决:请结合上述解题中所积累的经验和知识完成下题.如图,四边形ABCD中,AD⊥BD,AC⊥BC,AB与DC的延长线相交于点E,BE=BD,AB=5,AD=3,求CE的长.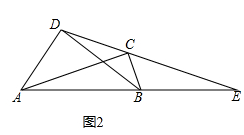
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b的图象经过点A(0,9),并且与直线y=
 x相交于点B,与x轴相交于点C.
x相交于点B,与x轴相交于点C.(1)若点B的横坐标为3,求B点的坐标和k,b的值;
(2)在y轴上是否存在这样的点P,使得以点P,B,A为顶点的三角形是等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.
(3)在直线y=kx+b上是否存在点Q,使△OBQ的面积等于
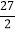 ?若存在,请求出点Q的坐标;若不存在,请说明理由.
?若存在,请求出点Q的坐标;若不存在,请说明理由.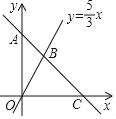
相关试题

