Question

【题目】如图，抛物线：y＝ax2＋bx＋4与x轴交于点A(－2，0)和B(4，0)、与y轴交于点C．

(1)求抛物线的解析式；

(2)T是抛物线对称轴上的一点，且△ACT是以AC为底的等腰三角形，求点T的坐标；

(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行．当点M原点时，点Q立刻掉头并以每秒个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动．过点M的直线l⊥轴，交AC或BC于点P．求点M的运动时间t(秒)与△APQ的面积S的函数关系式，并求出S的最大值．

Answer 1

【答案】（1）抛物线的解析式是y=x2+x+4；

（2）点T的坐标是(1，1)；

(3)点M的运动时间t与△APQ面积S的函数关系式是S=t2+6t(0<t2),S=t2+4t+3(2<t3),S的最大值是.

【解析】试题分析：（1）把A、B的坐标代入抛物线的解析式得到方程组，求出方程组的解即可；（2）设直线x=1上一点T（1，h），连接TC、TA，作CE⊥直线x=1，垂足是E，根据TA=TC由勾股定理求出即可；（3）（I）当0<t≤2时，△AMP∽△AOC，推出比例式，求出PM，AQ，根据三角形的面积公式求出即可；（II）当2<t≤3时，作PM⊥x轴于M，PF⊥y轴于点F，表示出三角形APQ的面积，利用配方法求出最值即可．

试题解析：(1)把A(2，0)，B(4，0)代入y=ax2+bx+4得：

，

解得：a=，b=1，

∴抛物线的解析式是：y=x2+x+4，

答：抛物线的解析式是y=x2+x+4.

(2)由y=x2+x+4= (x1)2+，得抛物线的对称轴为直线x=1，

直线x=1交x轴于点D，直线x=1上一点T(1，h)，

连接TC、TA，作CE⊥直线x=1，垂足是E，

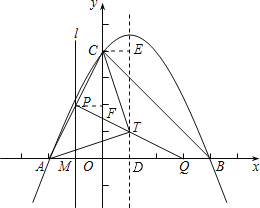
由C(0，4)得点E(1，4)，

在Rt△ADT和Rt△TEC中,由TA=TC得32+h2=12+(4h)2，

∴h=1，

∴T的坐标是(1，1)，

答：点T的坐标是(1，1).

(3)(I)当0<t2时，△AMP∽△AOC，

∴，PM=2t，

AQ=6t，

∴S=PMAQ=×2t(6t)=t2+6t=(t3)2+9，

当t=2时S的最大值为8；

(II)当2<t3时，

作PM⊥x轴于M，作PF⊥y轴于点F，

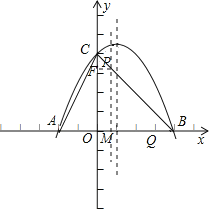
则△COB∽△CFP，

又∵CO=OB，

∴FP=FC=t2，PM=4(t2)=6t，AQ=4+32(t2)=32t+1，

∴S=PMAQ= (6t)( t+1)= t2+4t+3= (t)2+，

当t=时,S最大值为，

综合(I)(II)S的最大值为，

答：点M的运动时间t与△APQ面积S的函数关系式是S=t2+6t(0<t2),S=t2+4t+3(2<t3),S的最大值是.