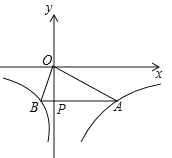
【题目】已知函数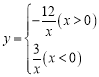 的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;
②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;
③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;
④当点P移动到使∠AOB=90°时,点A的坐标为(![]() ,
,![]() ).
).
其中正确的结论个数为( )
A.1 B.2 C.3 D.4
参考答案:
【答案】C.
【解析】
试题分析:①错误.∵x1<x2<0,函数y随x是增大而减小,∴y1>y2,故①错误.
②正确.∵P(0,﹣3),∴B(﹣1,﹣3),A(4,﹣3),∴AB=5,OA=![]() =5,∴AB=AO,∴△AOB是等腰三角形,故②正确.
=5,∴AB=AO,∴△AOB是等腰三角形,故②正确.
③正确.设P(0,m),则B(![]() ,m),A(﹣
,m),A(﹣![]() ,m),∴PB=﹣
,m),∴PB=﹣![]() ,PA=﹣
,PA=﹣![]() ,∴PA=4PB,∵SAOB=S△OPB+S△OPA=
,∴PA=4PB,∵SAOB=S△OPB+S△OPA=![]() =7.5,故③正确.
=7.5,故③正确.
④正确.设P(0,m),则B(![]() ,m),A(﹣
,m),A(﹣![]() ,m),∴PB=﹣
,m),∴PB=﹣![]() ,PA=﹣
,PA=﹣![]() ,OP=﹣m,∵∠AOB=90°,∠OPB=∠OPA=90°,∴∠BOP+∠AOP=90°,∠AOP+∠OPA=90°,∴∠BOP=∠OAP,∴△OPB∽△APO,∴
,OP=﹣m,∵∠AOB=90°,∠OPB=∠OPA=90°,∴∠BOP+∠AOP=90°,∠AOP+∠OPA=90°,∴∠BOP=∠OAP,∴△OPB∽△APO,∴![]() ,∴OP2=PBPA,∴m2=﹣
,∴OP2=PBPA,∴m2=﹣![]() (﹣
(﹣![]() ),∴m4=36,∵m<0,∴m=﹣
),∴m4=36,∵m<0,∴m=﹣![]() ,∴A(
,∴A(![]() ,﹣
,﹣![]() ),故④正确,∴②③④正确,故选C.
),故④正确,∴②③④正确,故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明到某公司应聘,他想了解自己入职后的工资情况,他需要关注该公司所有员工工资的( )
A.众数B.中位数C.方差D.平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,以
,以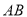 为直径作圆
为直径作圆 ,分别交
,分别交 于点
于点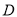 ,交
,交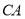 的延长线于点
的延长线于点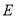 ,过点
,过点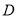 作
作 于点
于点 ,连接
,连接 交线段
交线段 于点
于点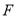 .
.(1)求证:
 是圆
是圆 的切线;
的切线;(2)若
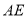 为
为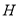 的中点,求
的中点,求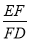 的值;
的值;(3)若
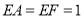 ,求圆
,求圆 的半径.
的半径.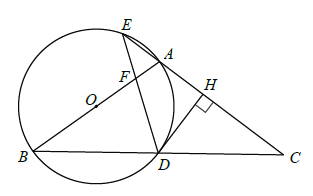
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.

(1)求证:BD∥EF;
(2)若点G是DC的中点,BE=6,求边AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车收费标准为:起步价(3千米以内或3千米)10元,3千米后每千米价1.8元,则某人乘坐出租车x(x>3)千米需付费( )元.
A. 10+1.8xB. 3+1.8x
C. 10+1.8(x﹣3)D. 3+1.8(x﹣3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.一个角的补角一定大于这个角B.平行于同一条直线的两条直线平行
C.等边三角形是中心对称图形D.旋转改变图形的形状和大小
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,请看下面的案例.
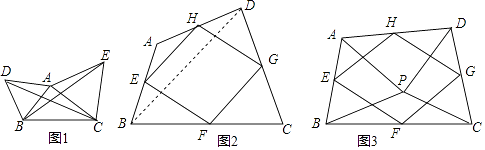
(1)如图1,已知△ABC,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BE.
通过证明△ ADC ≌△ ABE ,得到DC=BE;
(2)如图2,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,顺次连接E、F、G、H,得到四边形EFGH,我们称四边形EFGH为四边形ABCD的中点四边形,连接BD,利用三角形中位线的性质,可得EH∥BD,EH= BD,同理可得FG∥BD,FG=
BD,同理可得FG∥BD,FG=  BD,所以EH∥FG,EH=FG,所以四边形EFGH是平行四边形;
BD,所以EH∥FG,EH=FG,所以四边形EFGH是平行四边形;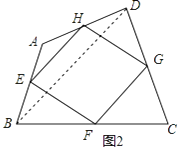
拓展应用
①如图3,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,四边形EFGH的形状是 .
相关试题

