【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作圆
为直径作圆![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)若![]() ,求圆
,求圆![]() 的半径.
的半径.
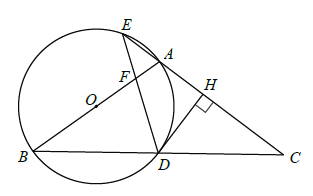
参考答案:
【答案】(1)证明见解析(2)![]() ,(3)
,(3)![]()
【解析】
试题分析:(1)连接OD,然后可得等腰三角形,然后通过等腰三角形的性质求得OD∥AC,然后可根据切线的判定求证即可;
(2)根据等腰三角形的性质和三角形的中位线可证得△AEF∽△ODF,由相似三角形的性质可求解;
(3)根据等腰三角形的性质,和圆的有关性质,可证明△BFD∽△EFA,然后根据相似三角形的性质可求解.
试题解析:(1)
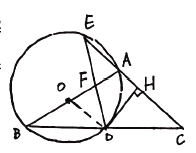
连接![]() ,
,
∵![]() ,
,
∴![]() 是等腰三角形,
是等腰三角形,
![]() ①,
①,
又在![]() 中, ∵
中, ∵![]() ,
,
∴![]() ②,
②,
则由①②得,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
(2)
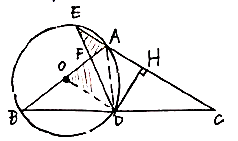
在![]() 中, ∵
中, ∵![]() ,
,
∵由![]() 中可知,
中可知,![]() ,
,
![]() 是等腰三角形,
是等腰三角形,
又∵![]() 且点
且点![]() 是
是![]() 中点,
中点,
∴设![]() ,则
,则![]() ,
,
连接![]() ,则在
,则在![]() 中,
中,![]() ,即
,即![]() ,
,
又∵![]() 是等腰三角形,∴
是等腰三角形,∴![]() 是
是![]() 中点,
中点,
则在![]() 中,
中,![]() 是中位线, ∴
是中位线, ∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
在![]() 和
和![]() 中,
中,![]() , ∴
, ∴![]() ,
,
∴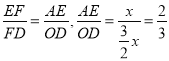 ,
,
∴![]() .
.
(3)设![]() 半径为
半径为![]() ,即
,即![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
又∵![]() , ∴
, ∴![]() ,
,
则![]() , ∴
, ∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中, ∵
中, ∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 是等腰三角形,
是等腰三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中
中![]() ,∵
,∵![]() ,
,
∴![]() ,
,
解得![]() (舍)
(舍)
∴综上,![]() 的半径为
的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=25,b=﹣3,则a99+b100的末位数字是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式是完全平方式的是( )
A.x2+2x﹣1
B.1+x2
C.x+xy+1
D.x2+2x+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明到某公司应聘,他想了解自己入职后的工资情况,他需要关注该公司所有员工工资的( )
A.众数B.中位数C.方差D.平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.

(1)求证:BD∥EF;
(2)若点G是DC的中点,BE=6,求边AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
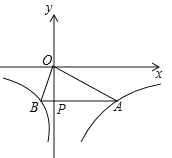
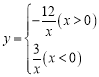 的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;
②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;
③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;
④当点P移动到使∠AOB=90°时,点A的坐标为(
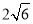 ,
,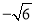 ).
).其中正确的结论个数为( )
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车收费标准为:起步价(3千米以内或3千米)10元,3千米后每千米价1.8元,则某人乘坐出租车x(x>3)千米需付费( )元.
A. 10+1.8xB. 3+1.8x
C. 10+1.8(x﹣3)D. 3+1.8(x﹣3)
相关试题

