Question

【题目】【问题背景】

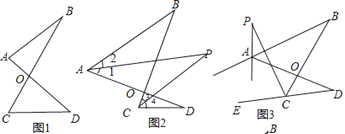
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；

【简单应用】

（2）如图2，AP、CP分别平分∠BAD．∠BCD，若∠ABC=36°，∠ADC=16°，

求∠P的度数；

【问题探究】

（3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．

【拓展延伸】

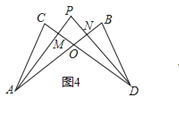
（4）在图4中，若设∠C=α，∠B=β，∠CAP=∠CAB，∠CDP=∠CDB，试问∠P与∠C、∠B之间的数量关系为： ______ （用α、β表示∠P,不必证明）

Answer 1

【答案】∠P=α+β.

【解析】试题分析：（1）根据三角形内角和定理即可证明．

（2）根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据（1）的结论列出整理即可得解；

（3）表示出∠PAD和∠PCD，再根据（1）的结论列出等式并整理即可得解；

（4）列出方程组即可解决问题．

试题解析：（1）证明：在△AOB中，∠A+∠B+∠AOB=180°，

在△COD中，∠C+∠D+∠COD=180°，

∵∠AOB=∠COD，∴∠A+∠B=∠C+∠D；

(2) 如图2，∵AP、CP分别平分∠BAD、∠BCD，
∴∠1=∠2，∠3=∠4，
∵∠2+∠B=∠3+∠P，
∠1+∠P=∠4+∠D，
∴2∠P=∠B+∠D，
∴∠P=（∠B+∠D）=×（36°+16°）=26°；

(3)如图3，

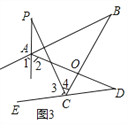
∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，

∴∠1=∠2，∠3=∠4，∴∠PAD=180°-∠2，∠PCD=180°-∠3，

∵∠P+（180°-∠1）=∠D+（180°-∠3），∠P+∠1=∠B+∠4，

∴2∠P=∠B+∠D，

∴∠P=（∠B+∠D）=×（36°+16°）=26°；

(4)∠P=α+β.