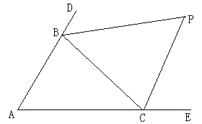
【题目】(12分)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=50°,则∠P= °;
(2)若∠A=90°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系,并说明理由。
参考答案:
【答案】解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,∠DBC+∠BCE=360°-130°=230°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC=![]() ∠DBC,∠PCB=
∠DBC,∠PCB=![]() ∠ECB,
∠ECB,
∴∠PBC+∠PCB=![]() (∠DBC+∠ECB)=115°,
(∠DBC+∠ECB)=115°,
∴∠P=65°.
同理得:(2)45°;
(3)40°
(4)∠P=90°-![]() ∠A.理由如下:
∠A.理由如下:
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°+![]() ∠A
∠A
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°-![]() ∠A.
∠A.
【解析】试题分析:(1)若∠A=50°,则有∠ABC+∠ACB=130°,∠DBC+∠BCE=360°-130°=230°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数;
(2)、(3)和(1)的解题步骤类似;(4)利用角平分线的性质和三角形的外角性质可求出∠BCP=![]() (∠A+∠ABC),∠CBP=
(∠A+∠ABC),∠CBP=![]() (∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.
(∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m>0,并且使得x2+2(m﹣2)x+16是完全平方式,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=
 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,∠1=∠2,∠B=35°,将求∠BDG的过程填写完整。
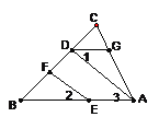
解: ∵EF∥AD,
∴∠2=____ (________________________________)
又∵∠1=∠2
∴∠1= ( 等量代换 )
∴DG∥_____ (___________________________________)
∴∠B+______=180°(___________________________)
∵∠B=35°
∴∠BDG =_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠XOY=90°,点A,B分别在射线OX,OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.试问∠ACB的大小是否变化?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(-2ax2)2-4ax3·(ax-1)= ___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】要想统计本班学生最喜欢的动画片,下面收集数据的方法较合适的是( )
A. 问卷调查 B. 访问 C. 观察 D. 查阅资料
相关试题

