【题目】如图,在平面直角坐标系xOy中,一次函数y=![]() x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问![]() 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
参考答案:
【答案】解:(1)∵y=![]() x+m经过点(-3,0),
x+m经过点(-3,0),
∴0=![]() +m,解得m=
+m,解得m=![]() ,
,
∴直线解析式为y=![]() x+
x+![]() ,C(0,
,C(0,![]() ).
).
∵抛物线y=ax2+bx+c对称轴为x=1,且与x轴交于A(-3,0),∴另一交点为B(5,0),
设抛物线解析式为y=a(x+3)(x-5),
∵抛物线经过C(0,![]() ),
),
∴![]() =a3(-5),解得a=
=a3(-5),解得a=![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x+
x+![]() ;
;
(2)要使△ACP的周长最小,只需AP+CP最小即可.如图2,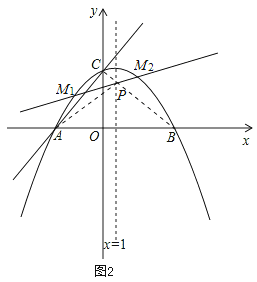
连接BC交x=1于P点,因为点A、B关于x=1对称,根据轴对称性质以及两点之间线段最短,可知此时AP+CP最小(AP+CP最小值为线段BC的长度).
∵B(5,0),C(0,![]() ),
),
∴直线BC解析式为y=![]() x+
x+![]() ,
,
∵xP=1,∴yP=3,即P(1,3).
(3) (3)存在 设Q(x, ![]() x2+
x2+![]() x+
x+![]() )
)
①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2
②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2
∴Q的横坐标为5.2 ,7.2
(4)令经过点P(1,3)的直线为y=kx+b,则k+b=3,即b=3-k,
则直线的解析式是:y=kx+3-k,
∵y=kx+3-k,y=![]() x2+
x2+![]() x+
x+![]() ,
,
联立化简得:x2+(4k-2)x-4k-3=0,
∴x1+x2=2-4k,x1x2=-4k-3.
∵y1=kx1+3-k,y2=kx2+3-k,∴y1-y2=k(x1-x2).
根据两点间距离公式得到:![]() =
=![]() =
=![]()
∴![]() =
=![]() =4(1+k2).
=4(1+k2).
又![]() =
=![]() =
=![]()
;
同理![]()
∴![]() =
=![]()
=![]()
=4(1+k2).
∴M1PM2P=M1M2 ,
∴![]() =1为定值.
=1为定值.
【解析】
(1)首先求得m的值和直线的解析式,根据抛物线对称性得到B点坐标,根据A、B点坐标利用交点式求得抛物线的解析式;
(2)确定何时△ACP的周长最小.利用轴对称的性质和两点之间线段最短的原理解决;确定P点坐标P(1,3),从而直线M1M2的解析式可以表示为y=kx+3-k;
(3)存在, 设Q(x,![]() x2+
x2+![]() x+
x+![]() )①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2,②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2从而求出Q点坐标.
)①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2,②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2从而求出Q点坐标.
(4)利用两点间的距离公式,分别求得线段M1M2、M1P和M2P的长度,相互比较即可得到结论:![]() =1为定值.
=1为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.

(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF;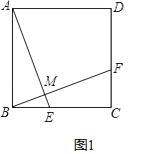
(2)如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论.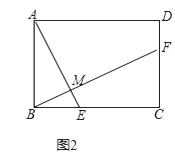
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C  在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了了解2018年初中毕业生毕业后的去向,对部分九年级学生进行了抽样调查,就九年级学生的四种去向(A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他)进行数据统计,并绘制了两幅不完整的统计图(如图①②)请问:

(1)本次共调查了_ 名初中毕业生;
(2)请计算出本次抽样调查中,读职业高中的人数和所占百分比,并将两幅统计图中不完整的部分补充完整;
(3)若该县2018年九年级毕业生共有
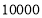 人,请估计该县今年九年级毕业生读职业高中的学生人数.
人,请估计该县今年九年级毕业生读职业高中的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
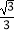 x2﹣
x2﹣ 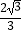 x﹣
x﹣ 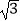 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.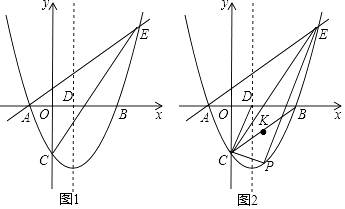
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=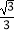 x2﹣
x2﹣ 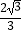 x﹣
x﹣ 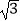 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
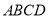 的对角线
的对角线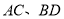 交于点
交于点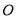 ,且
,且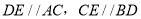 .
.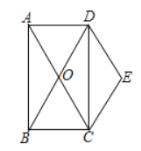
(1)求证:四边形
 是菱形;
是菱形;(2)若
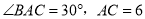 ,求菱形
,求菱形 的面积.
的面积.
相关试题

