【题目】如图,CD是AB上的高,AC=4,BC=3,DB= ![]() ,请判断△ABC的形状,并说明理由.
,请判断△ABC的形状,并说明理由. 
参考答案:
【答案】解:△ABC为直角三角形,理由如下: ∵CD⊥AB,
∴∠ADC=90°,
在Rt△BCD中,BC=3,DB= ![]() ,
,
根据勾股定理得:CD= ![]() =
= ![]() ,
,
在Rt△ACD中,AC=4,CD= ![]() ,
,
根据勾股定理得:AD= ![]() =
= ![]() ,
,
∴AB=BD+AD=5,
∵AC2+BC2=9+16=25,AB2=25,
∴AC2+BC2=AB2 ,
则△ABC为直角三角形
【解析】三角形ABC为直角三角形,理由为:根据CD与AB垂直,得到三角形BCD与三角形ACD都为直角三角形,利用勾股定理求出CD的长,继而求出AD的长,由BD+AD求出AB的长,再利用勾股定理的逆定理判断即可.
【考点精析】解答此题的关键在于理解勾股定理的逆定理的相关知识,掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.(a3)4=a12
B.a3a5=a15
C.a2+a2=a4
D.a6÷a2=a3 -
科目: 来源: 题型:
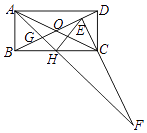
查看答案和解析>>【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE , ⑤CF=BD.正确的有( )个.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】多项式6πa3b2c2﹣x3y3z+m2n﹣110的次数是( )
A.10次
B.8次
C.7次
D.9次 -
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点.
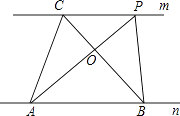
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.
(1)直接写出抛物线的顶点坐标;
(2)求抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x2+2=6x化成一般形式后,二次项系数和一次项系数分别是( )
A. 3、-6B. 3、6C. 3、2D. 2、-6
相关试题

