搜索
【题目】方程x2﹣3x+2＝0的解是（ ）
A. x1＝1，x2＝2B. x1＝﹣1，x2＝﹣2
C. x1＝1，x2＝﹣2D. x1＝﹣1，x2＝2
参考答案：
【答案】A
【解析】
将方程左边的多项式利用十字相乘法分解因式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程，求出一次方程的解即可得到原方程的解．
解：原方程可化为：（x﹣1）（x﹣2）＝0,
∴x1＝1，x2＝2．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，直线
交
轴于点A，交
轴于点C（0,4）.抛物线
经过点A，交
轴于点B（0，-2）.点P为抛物线上一个动点，经过点P作轴的垂线PD，过点B作BD⊥PD于点D，连接PB，设点P的横坐标为
.（1）求抛物线的解析式；
（2）当△BDP为等腰直角三角形时，求线段PD的长；
（3）如图2，将△BDP绕点B逆时针旋转，得到△BD′P′，且旋转角∠PBP′=∠OAC，当点P的对应点P′落在坐标轴上时，请直接写出点P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着信息技术的快速发展，“互联网＋”渗透到我们日常生活的各个领域，网上在线学习交流已不再是梦，现有某教学网站策划了A、B两种上网学习的月收费方案：
A方案：月租7元，可上网25小时，若超时，超出部分按每分钟0.01元收费；
B方案：月租10元，可上网50小时，若超时，超出部分按每分钟0.01元收费；
设每月上网学习时间为
小时.（1）当
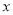＞50时，用含有x的代数式分别表示A、B两种上网的费用；（2）当x＝100时，分别求出两种上网学习的费用.
（3）若上网40小时，选择哪种方式上网学习合算，为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若点A(n，2)在y轴上，则点B(2n－1，3n+1)位于（ ）
A.第四象限．B.第三象限C.第二象限D.第一象限
-
科目： 来源： 题型：
查看答案和解析>>【题目】随地球自转，一天中太阳东升西落，太阳经过
某地天空的最高点时为此地的“地方时间”12点，
因此，不同经线上具有不同的“地方时间”．两个
地区“地方时间”之间的差称为这两个地区的时差．
右图表示同一时刻的韩国首尔时间和北京时间，
两地时差为整数．
（1）下表是同一时刻的北京和首尔的时间，请填写完整．
北京时间
7：30
首尔时间
12：15
（2）设北京时间为x（时），首尔时间为y（时），0≤x≤12时，求y关于x的函数表达式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】
如图，抛物线L:
（常数t>0）与x轴从左到右的交点为B，A，过线段OA的中点M作MP⊥x轴，交双曲线
于点P，且OA·MP=12.（1）求k值；
（2）当t=1时，求AB长，并求直线MP与L对称轴之间的距离；
（3）把L在直线MP左侧部分的图象（含与直线MP的交点）记为G，用t表示图象G最高点的坐标；
（4）设L与双曲线有个交点的横坐标为x0，且满足4≤x0≤6，通过L位置随t变化的过程，直接写出t的取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某同学利用描点法画二次函数y＝ax2+bx+c（a≠0）的图象时，列出的部分数据如下表：经检查，发现表格中恰好有一组数据计算错误，请你根据上述信息写出该二次函数的解析式：_____
x
0
1
2
3
4
y
3
0
﹣2
0
3
相关试题
