【题目】已知点A(a,0)和B(0,b)满足(a-4)2+|b-6|=0,分别过点A、B作x轴、y轴的垂线交于点C,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,直接写出点P的坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到BP,若BP将四边形OACB的面积分成相等的两部分,求h的值.

参考答案:
【答案】(1)A(4,0),B(0,6),C(4,6);(2)P(4,4);(3)h的值为2.
【解析】
(1)根据非负数的性质列式求出a、b的值,然后写出点A、B的坐标,再根据矩形的性质写出点C的坐标;
(2)求出点P运动的路程,然后确定出点P在AC边上并求出AP的值,再写出点P的坐标即可;
(3)根据平移的性质和矩形的性质表示出BB′、CP′然后根据面积公式列出方程求解即可.
解:(1)由非负数的性质得,a-4=0,b-6=0,
解得a=4,b=6,
所以,A(4,0),B(0,6),C(4,6);
(2)点P运动的路程=2×6=12,
所以,点P在边AC上,
AP=6+4+6-12=4,
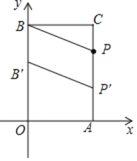
P点的位置如图:P(4,4);
(3)如图:∵PP′=BB′=h,
∴CP′=h+2,
∵B′P′将四边形OACB的面积分成相等的两部分,
∴![]() (h+h+2)4=
(h+h+2)4=![]() ×4×6,
×4×6,
解得h=2.
答:h的值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC=
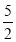 ,BC=4,点B在y轴上,BC∥x轴,反比例函数
,BC=4,点B在y轴上,BC∥x轴,反比例函数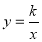 (x>0)的图像经过点A,交BC于点D.
(x>0)的图像经过点A,交BC于点D.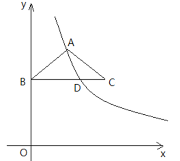
(1)若OB=3,求k的值;
(2)连接CO,若AB=BD,求四边形ABOC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的边BC上一点,连接DE,将DE绕着点E逆时针旋转90°,得到EG,过点G作GF⊥CB,垂足为F,GH⊥AB,垂足为H,连接DG,交AB于I.

(1)求证:四边形BFGH是正方形;
(2)求证:ED平分∠CEI;
(3)连接IE,若正方形ABCD的边长为3
 ,则△BEI的周长为 .
,则△BEI的周长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决问题
进位制是一种记数方式,可以用有限的数字符号代表所有的数值,使用数字符号的数目称为基数,基数为n,即可称n进制。现在最常用的是十进制,通常使用10个阿拉伯数字0~9进行记数,特点是逢十进一。
对于任意一个用
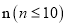 进制表示的数,通常使用n个阿拉伯数字
进制表示的数,通常使用n个阿拉伯数字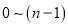 进行记数,特点是逢n进一。我们可以通过以下方式把它转化为十进制:
进行记数,特点是逢n进一。我们可以通过以下方式把它转化为十进制:例如:五进制数
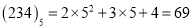 ,记作:
,记作:  ,
,七进制数
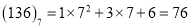 ,记作:
,记作: 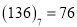
(1)请将以下两个数转化为十进制:
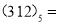 ____________,
____________, 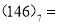 ____________ ;
____________ ;(2)若一个正数可以用七进制表示为
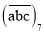 ,也可以用五进制表示为
,也可以用五进制表示为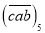 ,请求出这个数并用十进制表示。
,请求出这个数并用十进制表示。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,求∠BCE的度数;
(2)如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE的度数;
(3)设∠BAC=α,∠BCE=β,如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD.

(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
相关试题

