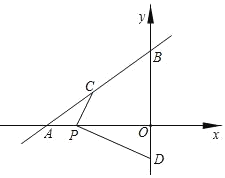
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
(1)点C的坐标为 ,点D的坐标为 ;
(2)点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.
参考答案:
【答案】(1)(-3,2);(0,-2)
(2)P(![]() ,0)
,0)
【解析】
(1)根据直线![]() 与C、D两点到x轴的距离均为2即可求出C,D的坐标;(2)连接CD,求出直线CD与x轴的交点即为P点.
与C、D两点到x轴的距离均为2即可求出C,D的坐标;(2)连接CD,求出直线CD与x轴的交点即为P点.
(1)令y=2,解得x=-3,∴点C的坐标为(-3,2)
令y=-2,解得x=0,∴点D的坐标为(0,-2)
(2)如图,连接CD,求出直线CD与x轴的交点即为P点.
设直线CD的解析式为y=kx+b,
把(-3,2),(0,2)代入得![]()
解得
∴y=![]() x-2
x-2
令y=0,解得x=![]()
∴P(![]() ,0)
,0)

-
科目: 来源: 题型:
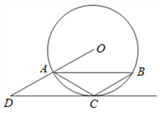
查看答案和解析>>【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB,CD与OA的延长线交于点D.
(1)求证:CD 是⊙O 的切线;
(2)若∠ACB=120°,OA=2,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)
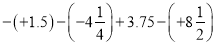
(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①AB//CD;②AB=CD;③BC//AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有哪几种,请一一写出_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我校七年级某班准备买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副
 元,乒乓球每盒
元,乒乓球每盒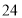 元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的
元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的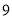 折优惠这个班级需要球拍
折优惠这个班级需要球拍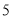 副,乒乓球
副,乒乓球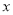 盒(
盒(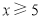 ).
).(1)分别求甲、乙两家商店购买这些商品所箭的费用(用含x的代数式表示);
(2)当
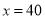 时,购买所需商品去哪家商店合算?请通过计算说明理由.
时,购买所需商品去哪家商店合算?请通过计算说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点C运动;点Q以1.25cm/s的速度沿BC向终点C运动,两点到达终点后停止运动。过点P作PE∥BC交AD于点E,连结EQ,设动点运动的时间为ts(t>0)。
(1) 连结DP,经过1s后,四边形EQDP能够成为平行四边形吗? 请说明理由;
(2) 当t为何值时,△EDQ为直角三角形?
(3) 如图②,设点M是EQ的中点,在点P、Q的整个运动过程中,试探究点M的运动路径长度是多少?

相关试题

