【题目】若存在正实数m,使得关于x的方程x+a(2x+2m﹣4ex)[ln(x+m)﹣lnx]=0成立,其中e为自然对数的底数,则实数a的取值范围是( )
A.(﹣∞,0)
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:由x+a(2x+2m﹣4ex)[ln(x+m)﹣lnx]=0得 x+2a(x+m﹣2ex)ln ![]() =0,
=0,
即1+2a( ![]() ﹣2e)ln
﹣2e)ln ![]() =0,
=0,
即设t= ![]() ,则t>0,
,则t>0,
则条件等价为1+2a(t﹣2e)lnt=0,
即(t﹣2e)lnt=﹣ ![]() 有解,
有解,
设g(t)=(t﹣2e)lnt,
g′(t)=lnt+1﹣ ![]() 为增函数,
为增函数,
∵g′(e)=lne+1﹣ ![]() =1+1﹣2=0,
=1+1﹣2=0,
∴当t>e时,g′(t)>0,
当0<t<e时,g′(t)<0,
即当t=e时,函数g(t)取得极小值为:g(e)=(e﹣2e)lne=﹣e,
即g(t)≥g(e)=﹣e,
若(t﹣2e)lnt=﹣ ![]() 有解,
有解,
则﹣ ![]() ≥﹣e,即
≥﹣e,即 ![]() ≤e,
≤e,
则a<0或a≥ ![]() ,
,
∴实数a的取值范围是(﹣∞,0)∪[ ![]() ,+∞).
,+∞).
故选:C.
【考点精析】根据题目的已知条件,利用特称命题的相关知识可以得到问题的答案,需要掌握特称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;特称命题的否定是全称命题.
;特称命题的否定是全称命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f(x0)=3,x0∈(
 ,
, 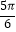 ),则sinx0的值为( )
),则sinx0的值为( ) 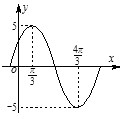
A.
B.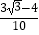
C.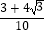
D.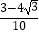
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,g(x)为定义在R上的奇函数,且当x<0时,g(x)=x2﹣2x﹣5,若f(g(a))≤2,则实数a的取值范围是( )
,g(x)为定义在R上的奇函数,且当x<0时,g(x)=x2﹣2x﹣5,若f(g(a))≤2,则实数a的取值范围是( )
A.
B. ??
??
C.(﹣∞,﹣1]∪(0,3]
D.[﹣1,3] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2,ADEF是正方形,在正方形ADEF内部有一点M,满足MB、MC与平面ADEF所成的角相等,则点M的轨迹长度为( )
A.
B.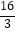
C.
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】若随机变量X~N(2,32),且P(X≤1)=P(X≥a),则(x+a)2(ax﹣
 )5展开式中x3项的系数是 .
)5展开式中x3项的系数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】半径为1的球O内有一个内接正三棱柱,当正三棱柱的侧面积最大时,球的表面积与该正三棱柱的侧面积之差是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,若3sinC=2sinB,点E,F分别是AC,AB的中点,则
 的取值范围为 .
的取值范围为 .
相关试题

