Question

【题目】如图，在ABCD中，点E在BC的延长线上，且CE=BC，AE=AB，AE、DC相交于点O，连接DE．

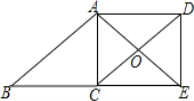
（1）求证：四边形ACED是矩形；

（2）若∠AOD=120°，AC=4，求对角线CD的长．

Answer 1

【答案】（1）证明见解析；（2）8．

【解析】

（1）根据平行四边形的性质得出AD∥BC，AD=BC，AB=DC，求出AD=CE，AD∥CE，AE=DC，根据矩形的判定得出即可；

（2）根据矩形的性质得出OAAE，OCCD，AE=CD，求出OA=OC，求出△AOC是等边三角形，即可得出答案．

（1）∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，AB=DC．

∵CE=BC，

∴AD=CE，AD∥CE，

∴四边形ACED是平行四边形．

∵AB=DC，AE=AB，

∴AE=DC，

∴四边形ACED是矩形；

（2）∵四边形ACED是矩形，

∴OAAE，OCCD，AE=CD，

∴OA=OC．

∵∠AOC=180°﹣∠AOD=180°﹣120°=60°，

∴△AOC是等边三角形，

∴OC=AC=4，

∴CD=8．