【题目】如图,在一次高尔夫球比赛中,小明从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度10m时,球移动的水平距离为8m.已知山坡OA与水平方向OC的夹角为30°,OC=12m.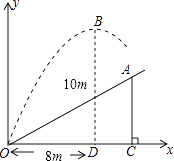
(1)求点A的坐标;
(2)求球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点.
参考答案:
【答案】
(1)
解:在Rt△ACO中,∠ACO=90°,∠AOC=30°,OC=12,
∴AC=OCtan∠AOC=12× ![]() =4
=4 ![]() ,
,
∴点A的坐标为(12,4 ![]() ).
).
(2)
解:∵顶点B的坐标为(8,10),
∴设球的飞行路线所在抛物线的解析式为y=a(x﹣8)2+10,
∵点O(0,0)在抛物线上,
∴0=a×(0﹣8)2+10,解得:a=﹣ ![]() ,
,
∴球的飞行路线所在抛物线的解析式为y=﹣ ![]() (x﹣8)2+10=﹣
(x﹣8)2+10=﹣ ![]() x2+
x2+ ![]() x.
x.
(3)
解:令y=﹣ ![]() x2+
x2+ ![]() x中x=12,则y=﹣
x中x=12,则y=﹣ ![]() ×122+
×122+ ![]() ×12=
×12= ![]() ,
,
∵ ![]() ≠4
≠4 ![]() ,
,
∴点A不在球的飞行路线所在抛物线上.
故小明这一杆不能把高尔夫球从O点直接打入球洞A点.
【解析】(1)在Rt△ACO中,根据特殊角的三角函数值求出AC的长度,由此即可得出点A的坐标;(2)由顶点B的坐标设球的飞行路线所在抛物线的解析式为y=a(x﹣8)2+10,根据点O的坐标利用待定系数法即可求出该抛物线的解析式;(3)代入x=12,求出当x=12时,抛物线上点的纵坐标,将其与点A的纵坐标进行比较,即可得出结论.
【考点精析】利用二次函数的图象对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________厘米/秒.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
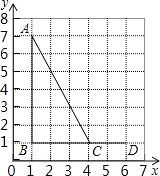
A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×4正方形网格中,有A,B,C三个格点(线与线的交点).

(1)若小正方形边长为1,则AC= , AB=;
(2)在图中再找出一个格点D,满足:D与A,B,C三点中的两点组成的三角形恰好与△ABC相似:∽△ABC. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个?
(1)AE平分∠DAB;(2)△EBA≌△DCE; (3)AB+CD=AD;(4)AE⊥DE;(5)AB//CD;
大家一起热烈地讨论交流,小红第一个得出正确答案,是( ).

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F.
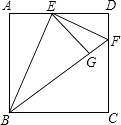
(1)若∠ABE:∠BFC=n,则n=;
(2)当E运动到AD中点时,求线段GF的长;
(3)若限定F仅在线段CD上(含端点)运动,直接写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【背景】国家为扶持软件企业的发展,对企业实行月补贴,以提高企业的净利润.
【问题】国内某软件企业2014 年12月份并未如期收到700万元的月补贴,这样导致2014 年的净利润增长只有55%.而若补贴及时到位,则2014 年的净利润增长将达到60%.
(1)求2013年该企业净利润是多少万元?
(2)又据统计,2014年12月该企业不含月补贴的月净利润为2100万元,2015年1月及2月不含月补贴的月净利润比上月增加的百分数分别是m和 2m,这两个月的月补贴相等,且都在2014年12月基础上增加了2m.据推算,若以后各月不含月补贴的月净利润和月补贴均稳定在2月份的水平不变,则 2015年该企业净利润将达到2013年的3倍,求m的值.
相关试题

