【题目】如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.
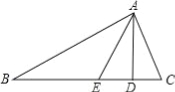
(1)求∠CAD、∠AEC和∠EAD的度数.
(2)若图形发生了变化,已知的两个角度数改为:当∠B=30°,∠C=60°则∠EAD= °;
当∠B=50°,∠C=60°时,则∠EAD= °;
当∠B=60°,∠C=60°时,则∠EAD= °;
当∠B=70°,∠C=60°时,则∠EAD= °.
(3)若∠B和∠C的度数改为用字母α和β来表示,你能找到∠EAD与α和β之间的关系吗?请直接写出你发现的结论.
参考答案:
【答案】(1)、∠CAD=30°,∠AEC=70°,∠EAD=20°;(2)、15°,5°,0°,5°;(3)、当α<β时,∠EAD=(β﹣α)°;当α>β时,∠EAD=(α﹣β)°
【解析】
试题分析:(1)、根据∠B和∠C的度数得出∠BAC的度数,根据角平分线的性质得出∠EAC的度数,根据高线的性质得出∠CAD的度数,根据∠EAD=∠EAC﹣∠DAC、∠AEC=180°﹣∠EAC﹣∠C得出角度;(2)、根据∠EAD=∠EAC﹣∠DAC或者∠EAD=∠DAC﹣∠EAC求出角度;(3)、当α<β时,根据∠EAD=∠EAC﹣∠DAC得出角度;当α>β时,根据∠EAD=∠DAC﹣∠EAC得出角度.
试题解析:(1)、∵∠B=20°,∠C=60°,
∴∠BAC=180°﹣20°﹣60°=100°,∵AE是角平分线,∴∠EAC=50°,
∵AD是高,∴∠ADC=90°,∴∠CAD=30°,
∴∠EAD=∠EAC﹣∠DAC=50°﹣30°=20°,
∴∠AEC=180°﹣∠EAC﹣∠C=180°﹣50°﹣60°=70°;
(2)、①∠EAD=∠EAC﹣∠DAC=45°﹣30°=15°;
②∠EAD=∠EAC﹣∠DAC=35°﹣30°=5°;
③∠EAD=∠EAC﹣∠DAC=30°﹣30°=0°;
④∠EAD=∠DAC﹣∠EAC=30°﹣25°=5°;
(3)当α<β时,
∴∠EAD=∠EAC﹣∠DAC=[(90﹣![]() )°﹣(90°﹣β°)]=(β﹣α)°
)°﹣(90°﹣β°)]=(β﹣α)°
当α>β时,
∴∠EAD=∠DAC﹣∠EAC=[(90°﹣β°)﹣(90﹣![]() )°]=(α﹣β)°
)°]=(α﹣β)°
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(x1,y1)和B(x2,y2)都在直线y=3x+2上,且x1>x2,则y1与y2的关系是( )
A. y1≤y2 B. y1≥y2 C. y1<y2 D. y1>y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示整数的点称为整数点,某数轴的单位长度是1㎝,若在这个数轴上随意画出一条长2009㎝的线段AB,被线段AB盖住的整数有( )
A.2006个或2007个
B.2007个或2008个
C.2008个或2009个
D.2009个或2010个 -
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
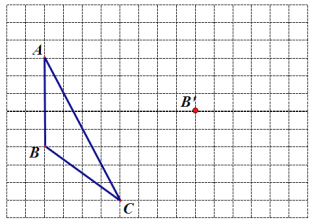
(1)请画出平移后的△A′B′C′.
(2)若连接AA′,CC′,则这两条线段之间的关系是________.
(3)利用网格画出△ABC 中AC边上的中线BD
(4)利用网格画出△ABC 中AB边上的高CE.
(5)△A′B′C′的面积为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道目前用超级计算机找到的最大质数是2859433-1,这个质数的末尾数字是( )
A.1
B.3
C.7
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产了5000个零件,从中抽取了50个零件做质量检查,在这一问题中( )
A. 5000个零件是总体 B. 50个是样本
C. 抽取的50个零件的质量是一个样本 D. 50个零件是样本容量
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程2x+3y﹣4=0,用含x的代数式表示y为__________
相关试题

