【题目】已知:如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12.在直线AC、BC上分别取一点M、N,使得△AMN≌△ABN,则CN=__________.
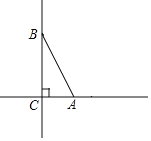
参考答案:
【答案】![]() 或
或![]() .
.
【解析】
分两种情况:①当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=13,求出CM,设CN=x,在Rt△MCN中,由勾股定理得出方程,解方程即可;
②当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=13,求出CM=18,设CN=x,则BN=MN=x+12,在Rt△MCN中,由勾股定理得出方程,解方程即可.
①如图1所示:

若△AMN≌△ABN,则BN=MN,且AM=AB=13,∴CM=8,
设CN=x,在Rt△MCN中,MC2+CN2=MN2,即82+x2=(12–x)2,
解得x= ![]() ,∴CN=
,∴CN= ![]() ;
;
②如图2所示:
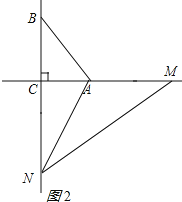
若△AMN≌△ABN,则BN=MN,且AM=AB=13,∴CM=18,
设CN=x,则BN=MN=x+12,
在Rt△MCN中,MC2+CN2=MN2,
即182+x2=(12+x)2,解得x= ![]() ,∴CN=
,∴CN= ![]() ;
;
综上所述:CN的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点
 是
是 的边
的边 上的一点,过点
上的一点,过点 作
作 ,
, ,
, ,
, 为垂足,再过点
为垂足,再过点 作
作 ,交
,交 于点
于点 ,且
,且 .
.
(1)求证:
 ;
;(2)求证:
 垂直平分
垂直平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,等边
 .
.(1)如图(1),若
 ,现有两点
,现有两点 、
、 分别从点
分别从点 、点
、点 同时出发,沿三角形的边顺时针运动,已知点
同时出发,沿三角形的边顺时针运动,已知点 的速度为
的速度为 ,点
,点 的速度为
的速度为 .当点
.当点 第一次到达
第一次到达 点时,
点时, 、
、 同时停止运动.点
同时停止运动.点 ,
, 运动______秒后,
运动______秒后, 为等腰三角形.
为等腰三角形.
(2)如图,点
 位于等边
位于等边 的内部,且
的内部,且 .将
.将 绕点
绕点 顺时针旋转
顺时针旋转 ,点
,点 的对应点为点
的对应点为点 .
.①依题意,补全图形;
②若
 ,
, ,求
,求 与
与 的面积比.
的面积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
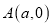 ,
,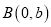 ,满足:
,满足: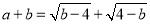 .
.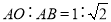 .
.(1)
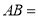 ______;
______;(2)点
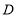 是
是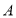 点左侧的
点左侧的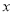 轴上一点,连接
轴上一点,连接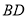 ,以
,以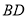 为直角边作等腰直角
为直角边作等腰直角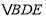 ,
,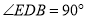 .连接
.连接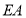 ,
,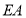 交
交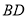 于点
于点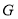 ;
;①求
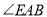 .
.②若
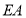 平分
平分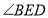 ,试求
,试求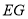 的长.
的长.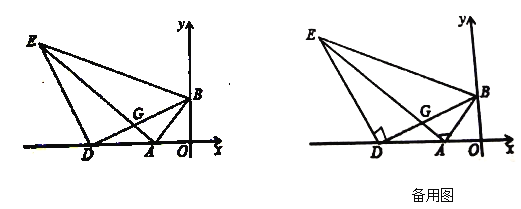
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )

A. 1 m B. 2 m C. 3 m D. 6 m
-
科目: 来源: 题型:
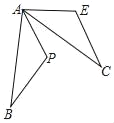
查看答案和解析>>【题目】(1)如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.
(2)解不等式组:
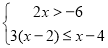
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
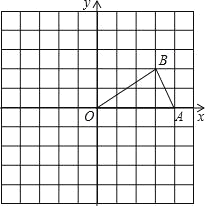
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
相关试题

