【题目】已知,如图AB∥CD,∠B=80°,∠BCE=20°,∠CEF=80°,请判断AB与EF的位置关系,并说明理由.

解:理由如下:
∵AB∥CD
∴∠B=∠BCD .
∵∠B=80°,
∴∠BCD=80° .
∵∠BCE=20°,
∴∠ECD=100°,
又∵∠CEF=80°
∴ + =180°,
∴EF∥
又∵AB∥CD,
∴AB∥EF .
参考答案:
【答案】AB∥EF,理由见解析;填空答案:AB∥EF,两直线平行,内错角相等;等量代换,∠E,∠DCE,CD,同旁内角互补,两直线平行;平行于同一直线的两条直线互相平行.
【解析】
根据平行线的性质,可得∠BCD=80°,进而可得到∠E+∠ECD=180°,可证明EF∥CD,由平行的“传递性”可证明结论.
AB∥EF,理由如下:
∵AB∥CD,
∴∠B=∠BCD,(两直线平行,内错角相等)
∵∠B=80°,
∴∠BCD=80°,(等量代换)
∵∠BCE=20°,
∴∠ECD=100°,
∵∠CEF=80°,
∴∠E+∠DCE=180°,
∴EF∥CD,(同旁内角互补,两直线平行)
∴AB∥EF.(平行于同一条直线的两条直线互相平行)
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
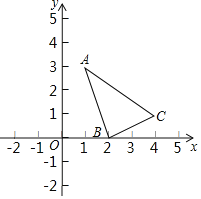
(1)分别写出下列三点坐标:A ,B ,C ;
(2)将△ABC平移至△OB′C′位置,使点A与原点O重合,画出平移后的△OB′C′,写出B′、C′的坐标;
(3)求△OB′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为__.
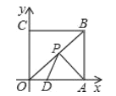
-
科目: 来源: 题型:
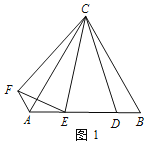
查看答案和解析>>【题目】【操作发现】如图 1,△ABC 为等边三角形,点 D 为 AB 边上的一点,∠DCE=30°,将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF,连接 AF、EF. 请直接 写出下列结果:
① ∠EAF的度数为__________;
② DE与EF之间的数量关系为__________;
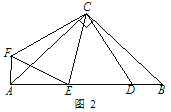
【类比探究】如图 2,△ABC 为等腰直角三角形,∠ACB=90°,点 D 为 AB 边上的一点∠DCE=45°,将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF,连接 AF、EF.
①则∠EAF的度数为__________;
② 线段 AE,ED,DB 之间有什么数量关系?请说明理由;
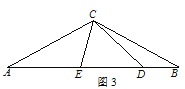
【实际应用】如图 3,△ABC 是一个三角形的余料.小张同学量得∠ACB=120°,AC=BC, 他在边 BC 上取了 D、E 两点,并量得∠BCD=15°、∠DCE=60°,这样 CD、CE 将△
ABC 分成三个小三角形,请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
-
科目: 来源: 题型:
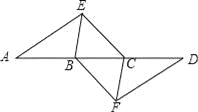
查看答案和解析>>【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,
 =3,n=
=3,n=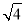 ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.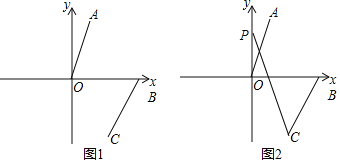
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
-
科目: 来源: 题型:
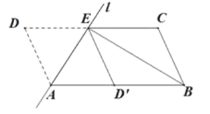
查看答案和解析>>【题目】如图,将
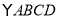 沿过点
沿过点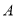 的直线
的直线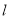 折叠,使点
折叠,使点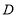 落到
落到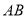 边上的
边上的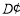 处,折痕交
处,折痕交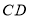 边于点
边于点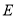 ,连接
,连接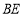 .
.
(1)求证:四边形
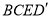 是平行四边形;
是平行四边形;(2)若
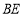 平分
平分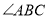 ,求证:
,求证: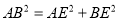 .
.
相关试题

