【题目】期中考试临近,某校初二年级教师对复习课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
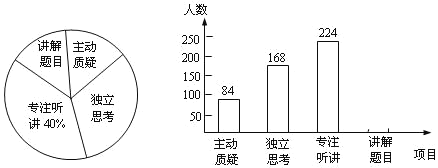
(1)在这次评价中,一共抽查了_________名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为______度;
(3)请将频数分布直方图补充完整;
(4)如果全市有8000名初二学生,那么在复习课中,“独立思考”的学生约有多少人?
参考答案:
【答案】(1)560,(2) 54°(3) 见解析(4)2400
【解析】
(1)由“专注听讲”的学生人数除以占的百分比求出调查学生总数即可;
(2)由“主动质疑”占的百分比乘以360°即可得到结果;
(3)求出“讲解题目”的学生数,补全统计图即可;
(4)求出“独立思考”学生占的百分比,乘以8000即可得到结果.
解:(1)根据题意得:224÷40%=560(名),
则在这次评价中,一个调查了560名学生;
故答案为:560;
(2)根据题意得:![]() ×360°=54°,
×360°=54°,
则在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为54度;
故答案为:54;
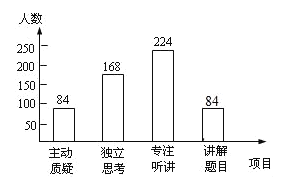
(3)“讲解题目”的人数为560﹣(84+168+224)=84,补全统计图如下:
(4)根据题意得:8000×![]() ×100%=2400(人),
×100%=2400(人),
则“独立思考”的学生约有2400人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明解不等式
 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,

(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下折痕EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数
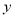 (件)与价格
(件)与价格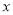 (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动 实验、猜想与证明
问题情境
(1)数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.

解决问题
(2)小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.
相关试题

