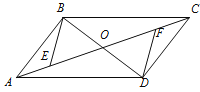
【题目】如图，□ABCD的对角线AC、BD相交于点O，AE＝CF．

（1）求证：△BOE≌△DOF；

（2）若BD＝EF，连接DE、BF，判断四边形EBFD的形状，并说明理由．

参考答案：

【答案】（1）证明见解析；（2）四边形EBFD为矩形，理由见解析．

【解析】试题分析：（1）先证出OE=OF，再由SAS即可证明△BOE≌△DOF；

（2）由对角线互相平分证出四边形EBFD是平行四边形，再由对角线相等，即可得出四边形EBFD是矩形．

试题解析：（1）证明：∵四边形ABCD为平行四边形，

∴BO＝DO，AO＝CO．

∵AE＝CF，

∴AO－AE＝CO－CF，即EO＝FO．

在△BOE与△DOF中

∴△BOE≌△DOF．

（2）四边形EBFD为矩形．

∵EO＝FO，BO＝DO，

∴四边形EBFD为平行四边形．

∵BD＝EF，

∴四边形EBFD为矩形．

关闭