【题目】已知二次函数y=x -2mx(m为常数),当-1≤x≤2时,函数y的最小值为-2,则m的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D. -
D. -![]() 或
或![]()
参考答案:
【答案】D
【解析】先将二次函数配方得: ![]() ,根据二次函数图象和性质可知:
,根据二次函数图象和性质可知:
对称轴![]() ,由于对称轴位置不确定,所以分m<-1, m>2, -1≤m≤2三种情况,根据二次函数y的最小值为-2,结合二次函数图象和性质进行解答, ①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-
,由于对称轴位置不确定,所以分m<-1, m>2, -1≤m≤2三种情况,根据二次函数y的最小值为-2,结合二次函数图象和性质进行解答, ①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-![]() ,②若m>2,当x=2时,y最小值=4-4m=-2,解得m=
,②若m>2,当x=2时,y最小值=4-4m=-2,解得m=![]() <2(舍),
<2(舍),
③若-1≤m≤2,当x=m时,y最小值=-![]() =-2,解得m=
=-2,解得m=![]() 或m=-
或m=-![]() <-1(舍),综上所述,m的值为-
<-1(舍),综上所述,m的值为-![]() 或
或![]() ,因此正确选项是D.
,因此正确选项是D.
y=x -2mx=(x-m) -m2.分以下3种情况:①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-![]() ;②若m>2,当x=2时,y最小值=4-4m=-2,解得m=
;②若m>2,当x=2时,y最小值=4-4m=-2,解得m=![]() <2(舍);③若-1≤m≤2,当x=m时,y最小值=-m2=-2,解得m=
<2(舍);③若-1≤m≤2,当x=m时,y最小值=-m2=-2,解得m=![]() 或m=-
或m=-![]() <-1(舍).综上所述,m的值为-
<-1(舍).综上所述,m的值为-![]() 或
或![]() ,故选D
,故选D
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A、B、O在数轴上对应的数为a、b、0,且满足|a+8|+(b﹣12)2=0,点M、N分别从O、B出发,同时向左匀速运动,M的速度为1个单位长度每秒,N的速度为3个单位长度每秒,A、B之间的距离定义为:AB=|a﹣b|.
(1)直接写出OA= .OB= ;
(2)设运动的时间为t秒,当t为何值时,恰好有AN=2AM;
(3)若点P为线段AM的中点,Q为线段BN的中点,M、N在运动的过程中,PQ+MN的长度是否发生变化?若不变,请说明理由,若变化,当t为何值时,PQ+MN有最小值?最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=
 (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p= ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=
 =6,∴S=
=6,∴S= =
= =6.
=6.事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
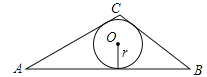
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数的三次方都可以分解为若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19.按此规律,若m3分解后,最后一个奇数为109,则m的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在函数
 与
与
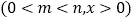 的图象上,对角线
的图象上,对角线 轴,且
轴,且 于点
于点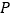 .已知点B的横坐标为4.
.已知点B的横坐标为4.
(1)当
 ,
, 时,
时,①若点P的纵坐标为2,求四边形ABCD的面积.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)当四边形ABCD为正方形时,直接写出m、n之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
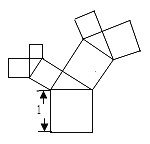
A.1B.2018C.2019D.2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡村距城市50km,甲骑自行车从乡村出发进城,出发1小时30分后,乙骑摩托车也从乡村出发进城,结果比甲先到1小时,已知乙的速度是甲的2.5倍,求甲、乙两人的速度。
【答案】甲速12km/h,乙速30km/h.
【解析】试题分析:设甲的速度是
 则乙的速度是
则乙的速度是 甲、乙所用时间分别为:
甲、乙所用时间分别为:  小时、
小时、 小时;根据题意可得甲比乙多用2.5小时,从而可得关于
小时;根据题意可得甲比乙多用2.5小时,从而可得关于 的方程,解方程即可解答此题;注意,最后要结合题意验根.
的方程,解方程即可解答此题;注意,最后要结合题意验根.试题解析:设甲的速度是
 则乙的速度是
则乙的速度是 根据题意列方程,得
根据题意列方程,得 整理,得
整理,得 ,
,解得:

经检验,
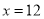 是原方程的解.
是原方程的解.则

答:甲的速度是12km/h,乙的速度是30km/h.
【题型】解答题
【结束】
24【题目】已知
 求
求 的值 。
的值 。
相关试题

