【题目】如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在函数![]() 与
与![]()
![]() 的图象上,对角线
的图象上,对角线![]() 轴,且
轴,且![]() 于点
于点![]() .已知点B的横坐标为4.
.已知点B的横坐标为4.

(1)当![]() ,
,![]() 时,
时,
①若点P的纵坐标为2,求四边形ABCD的面积.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)当四边形ABCD为正方形时,直接写出m、n之间的数量关系.
参考答案:
【答案】(1)①![]() ;②四边形ABCD是菱形,见解析;(2)
;②四边形ABCD是菱形,见解析;(2)![]() .
.
【解析】
(1)①先确定出点A,B,C,D坐标,再利用面积的求法即可得出结论;
②先确定出点D坐标,进而确定出点P坐标,进而求出PA,PC,即可得出结论;
(2)先确定出B(4,![]() ),D(4,
),D(4,![]() ),进而求出点P的坐标,再求出A,C坐标,最后用AC=BD,即可得出结论.
),进而求出点P的坐标,再求出A,C坐标,最后用AC=BD,即可得出结论.
解:(1)①![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵点B的横坐标为4,![]() .
.![]() .
.
![]() 轴,
轴,![]() ,点P的纵坐标为2,
,点P的纵坐标为2,
∴![]() ,
,![]() .
.![]() .
.
∴![]() ;
;
②四边形ABCD是菱形.
理由:![]() ,点P是线段BD的中点,
,点P是线段BD的中点,
![]() .
.
![]() 轴,
轴,![]() ,
,
![]()
∴![]() .
.![]() .
.
![]() ,∴四边形ABCD为平行四边形.
,∴四边形ABCD为平行四边形.
![]() ,∴四边形ABCD是菱形.
,∴四边形ABCD是菱形.
(2)![]() .
.
理由:当四边形ABCD是正方形,记AC,BD的交点为P,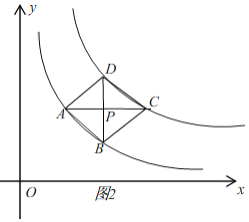
∴BD=AC
当x=4时,y=![]() =
=![]() , y=
, y=![]() =
=![]() ,
,
∴B(4,![]() ),D(4,
),D(4,![]() ),
),
∴P(4,![]() ),
),
∴A(![]() ,
, ![]() ),C(
),C(![]() ,
,![]() )
)
∵AC=BD,
∴![]() -
-![]() =
=![]() -
-![]() ,
,
∴m+n=32
故答案为:(1)①![]() ;②四边形ABCD是菱形,见解析;(2)
;②四边形ABCD是菱形,见解析;(2)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=
 (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p= ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=
 =6,∴S=
=6,∴S= =
= =6.
=6.事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
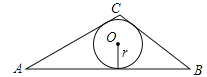
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数的三次方都可以分解为若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19.按此规律,若m3分解后,最后一个奇数为109,则m的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x -2mx(m为常数),当-1≤x≤2时,函数y的最小值为-2,则m的值是( )
A.
 B.
B.  C.
C.  或
或 D. -
D. - 或
或
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
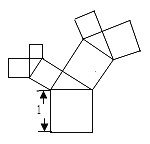
A.1B.2018C.2019D.2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡村距城市50km,甲骑自行车从乡村出发进城,出发1小时30分后,乙骑摩托车也从乡村出发进城,结果比甲先到1小时,已知乙的速度是甲的2.5倍,求甲、乙两人的速度。
【答案】甲速12km/h,乙速30km/h.
【解析】试题分析:设甲的速度是
 则乙的速度是
则乙的速度是 甲、乙所用时间分别为:
甲、乙所用时间分别为:  小时、
小时、 小时;根据题意可得甲比乙多用2.5小时,从而可得关于
小时;根据题意可得甲比乙多用2.5小时,从而可得关于 的方程,解方程即可解答此题;注意,最后要结合题意验根.
的方程,解方程即可解答此题;注意,最后要结合题意验根.试题解析:设甲的速度是
 则乙的速度是
则乙的速度是 根据题意列方程,得
根据题意列方程,得 整理,得
整理,得 ,
,解得:

经检验,
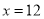 是原方程的解.
是原方程的解.则

答:甲的速度是12km/h,乙的速度是30km/h.
【题型】解答题
【结束】
24【题目】已知
 求
求 的值 。
的值 。 -
科目: 来源: 题型:
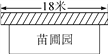
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若苗圃园的面积为72平方米,求x的值;
(2)若平行于墙的一边长不大于14米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
相关试题

