【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=5,BC=12,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠FME的度数.

参考答案:
【答案】(1)17;(2)60°
【解析】试题分析:(1)根据直角三角形的性质得到ME=MF=6,于是得到结论;
(2)根据等腰三角形的性质得到∠ABC=∠MFB=50°,∠ACB=∠MEC=70°,根据平角的定义和三角形的内角和得到结论.
试题解析:解:(1)∵CF⊥AB于F,M为BC的中点,
∴ME=MC=![]() BC=
BC=![]() ×12=6,
×12=6,
同理MF=MB=![]() BC=
BC=![]() ×12=6,
×12=6,
∴△EFM的周长=6+6+5=17;
(2)∵MF=MB,
∴∠ABC=∠MFB=50°,
同理∠ACB=∠MEC=70°,
∴∠BMF=180°﹣50°﹣50°=80°,
∠EMC=180°﹣70°﹣70°=40°,
∴∠FME=180°﹣80°﹣40°=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为( )
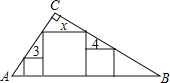
A.5
B.6
C.7
D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2㎝,BC=6㎝,AB=7㎝,点P是从点B出发在射线BA上的一个动点,运动的速度是1㎝/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
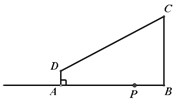
A.5个
B.4个
C.3个
D.2个
-
科目: 来源: 题型:
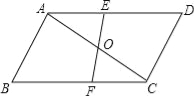
查看答案和解析>>【题目】如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1
B.2
C.3
D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=3x+2沿y轴向下平移4个单位,则平移后直线与y轴的交点坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果5x|m|y2﹣(m﹣2)xy﹣3x是关于x、y的四次三项式,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B在小正方形的顶点上.
(1)在直线l上找一点C,使它到A,B两点的距离相等;
(2)在(1)的基础上画出△ABC关于直线l成轴对称的△A′B′C′;
(3)在直线l上找一点P(在答题纸上图中标出),使PA+PB的长最短,这个最短长度的平方值是 .

相关试题

