【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
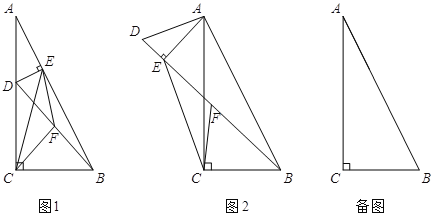
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
参考答案:
【答案】(1)k=1(2)证明![]() ,则可得
,则可得![]() . (3)当点D在靠近点C的
. (3)当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()
【解析】试题分析:解:(1)k=1; .
(2)如图2,过点C作CE的垂线交BD于点G,设BD与AC的交点为Q.
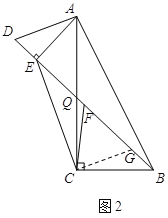
由题意,tan∠BAC=![]() ,
,
∴![]() .
.
∵D、E、B三点共线,
∴AE⊥DB.
∵∠BQC=∠AQD,∠ACB=90°,
∴∠QBC=∠EAQ.
∵∠ECA+∠ACG=90°,∠BCG+∠ACG=90°,
∴∠ECA=∠BCG.
∴![]() .
.
∴![]() .
.
∴GB=DE.
∵F是BD中点,
∴F是EG中点.
在![]() 中,
中, ![]() ,
,
∴![]() . . .
. . .
(3)情况1:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,
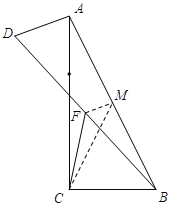
∵∠ACB=90°, tan∠BAC=![]() ,且BC= 6,
,且BC= 6,
∴AC=12,AB=![]() .
.
∵M为AB中点,∴CM=![]() ,
,
∵AD= ![]() ,
,
∴AD=![]() .
.
∵M为AB中点,F为BD中点,
∴FM= ![]() = 2.
= 2.
∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,此时CF=CM+FM=![]() .
.
情况2:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,
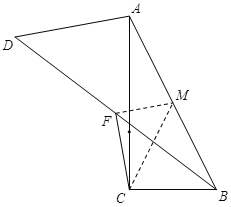
类似于情况1,可知CF的最大值为![]() .
.
. 6分
综合情况1与情况2,可知当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()
-
科目: 来源: 题型:
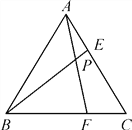
查看答案和解析>>【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象相交于点A(﹣2,1),点B(1,n).
的图象相交于点A(﹣2,1),点B(1,n).(1)求此一次函数和反比例函数的解析式;
(2)请直接写出满足不等式kx+b﹣
 <0的解集;
<0的解集;(3)在平面直角坐标系的第二象限内边长为1的正方形EFDG的边均平行于坐标轴,若点E(﹣a,a),如图,当曲线y=
 (x<0)与此正方形的边有交点时,求a的取值范围.
(x<0)与此正方形的边有交点时,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购买50根跳绳,如果A型跳绳的数量不多于B型跳绳数量的3倍,那么A型跳绳最多能买多少条?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
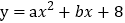 (a≠0)的图像与x轴交于点A(-2,0)、B,与y轴交于点C,tan∠ABC=2.
(a≠0)的图像与x轴交于点A(-2,0)、B,与y轴交于点C,tan∠ABC=2.(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
(3)在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
-
科目: 来源: 题型:
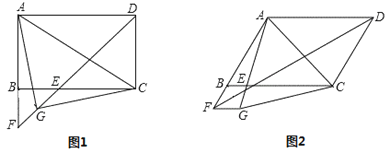
查看答案和解析>>【题目】在
 ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.
ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,判断△AGC的形状.(直接写出结论不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
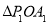 ,
,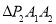 ,
,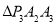 ,…都是等腰直角三角形,其直角顶点
,…都是等腰直角三角形,其直角顶点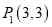 ,
,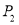 ,
,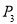 ,…均在直线
,…均在直线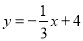 上.设
上.设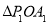 ,
,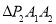 ,
,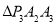 ,…的面积分别为
,…的面积分别为 ,
,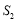 ,
,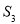 ,…,根据图形所反映的规律,
,…,根据图形所反映的规律,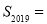 ( )
( )
A.
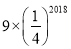 B.
B. 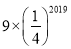 C.
C. 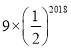 D.
D. 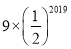
相关试题

