【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
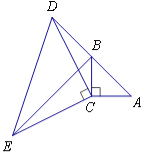
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE= cm;
(3)BE与AD有何位置关系?请说明理由.
参考答案:
【答案】(1)根据等腰直角三角形的性质可得CD=CE,由∠ACB=90°可得∠ACB=∠DCE,即可证得∠ACD=∠BCE,再结合AC=BC,即可证得结论;(2)6![]() ;(3)垂直
;(3)垂直
【解析】
试题(1)根据等腰直角三角形的性质可得CD=CE,由∠ACB=90°可得∠ACB=∠DCE,即可证得∠ACD=∠BCE,再结合AC=BC,即可证得结论;
(2)先由勾股定理求得AB=3![]() ,再由DB=AB,可得AD的长,然后根据全等三角形的性质求解即可;
,再由DB=AB,可得AD的长,然后根据全等三角形的性质求解即可;
(3)根据全等三角形的性质及三角形的面积公式求解即可
解:(1)∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∵AC=BC
∴△ACD≌△BCE;
(2)∵AC=BC=3,∠ACB=90°,由勾股定理得:AB=3![]() ,
,
又∵DB=AB,
∴AD=2AB=6![]() ,
,
∵△ACD≌△BCE;
∴BE=AD=6![]() cm;
cm;
(3)如图所示:
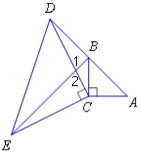
∵△ACD≌△BCE
∴∠ADC=∠BEC
∵∠1=∠2,∠DCE=90°
∴∠DBE=∠DCE=90°
∴BE⊥AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则
 周长的最小值为______.
周长的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店用1000元购进一批套尺,很快销售一空;商店又用1500元购进第二批同款套尺,购进单价比第一批贵25%,所购数量比第一批多100套.
(1)求第一批套尺购进的单价;
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有
 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为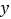 元(利润=收入-支出).
元(利润=收入-支出).(1)请写出
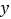 与
与 的关系式 ;
的关系式 ;(2)完成表格.
 人
人500
1000
1500
2000
2500
3000
…
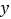 元
元…
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
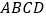 的边长
的边长  .某一时刻,动点
.某一时刻,动点 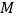 从
从 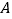 点出发沿
点出发沿 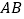 方向以
方向以 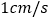 的速度向
的速度向 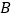 点匀速运动;同时,动点
点匀速运动;同时,动点 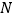 从
从 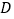 点出发沿
点出发沿 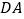 方向以
方向以 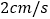 的速度向
的速度向 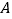 点匀速运动,问:
点匀速运动,问: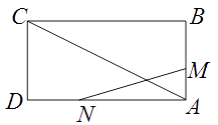
(1)经过多少时间, 的面积等于矩形
的面积等于矩形  面积的
面积的  ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,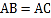 ,D在边AC上,且
,D在边AC上,且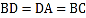 .
.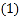 如图1,填空
如图1,填空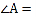 ______
______ ,
,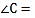 ______
______
 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线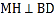 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E. 求证:
求证: 是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )
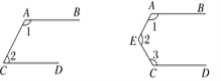

A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
相关试题

