【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为 . 
参考答案:
【答案】60°, ![]()
【解析】解:∵将△ABC绕点C按顺时针方向旋转n度后得到△EDC, ∴BC=DC,
∵在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=90°﹣∠A=60°,
∴△DBC是等边三角形,
∴n=∠DCB=60°,
∴∠DCA=90°﹣∠DCB=90°﹣60°=30°,
∵BC=2,
∴DC=2,
∵∠FDC=∠B=60°,
∴∠DFC=90°,
∴DF= ![]() DC=1,
DC=1,
∴FC= ![]() =
= ![]() ,
,
∴S阴影=S△DFC= ![]() DFFC=
DFFC= ![]() ×1×
×1× ![]() =
= ![]() .
.
所以答案是:60°, ![]() .
.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。

证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为 cm2 . (结果保留π)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=
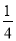 ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD. 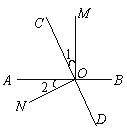
-
科目: 来源: 题型:
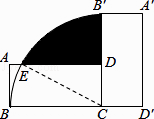
查看答案和解析>>【题目】如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
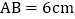 ,动点
,动点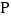 以
以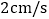 的速度从
的速度从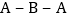 在线段
在线段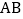 上运动,到达点
上运动,到达点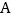 后,停止运动;动点
后,停止运动;动点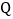 以
以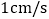 的速度从
的速度从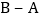 在线段
在线段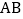 上运动,到达点
上运动,到达点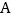 后,停止运动.若动点
后,停止运动.若动点 同时出发,设点
同时出发,设点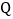 的运动时间是
的运动时间是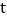 (单位:
(单位: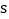 )时,两个动点之间的距离为S(单位:
)时,两个动点之间的距离为S(单位: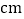 ),则能表示
),则能表示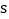 与
与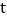 的函数关系的是( )
的函数关系的是( )
A.
 B.
B. 
C.
 D.
D. 
相关试题

