搜索
【题目】如图，点O是线段AB上一点，AB=4cm，AO=1cm，若线段AB绕点O顺时针旋转120°到线段A′B′的位置，则线段AB在旋转过程中扫过的图形的面积为 cm2 ． （结果保留π）
参考答案：
【答案】
【解析】解：由题意得：OA=1，OB=3； ∵S扇形A′OA= 
= 
，S扇形BOB′= 
=3π，
∴线段AB在旋转过程中扫过的图形的面积= +π= （cm2），
所以答案是 ．
【考点精析】关于本题考查的扇形面积计算公式和旋转的性质，需要了解在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，AD=2
，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为 ．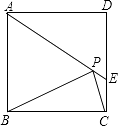 
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，D是等边三角形ABC边BA上一动点（点D）与点B不重合，连接CD，以CD为边在BC上方作等边三角形DCE，连接AE，你能发现AE与BD之间的数量关系吗？并证明你发现的结论．
（2）如图二，当动点D在等边三角形ABC边BA上运动时（点D与点B不重合），连接DC，以DC为边在其上方、下方分别作等边三角形DCE和等边三角形DCF，连接AE，BF，探究AE，BF与AB有何数量关系？并证明你探究的结论．
（3）如图三，当动点D在等边三角形ABC边BA的延长线上运动时，其他作法与图2相同，若AE＝8，BF＝2，请直接写出AB＝ ．
-
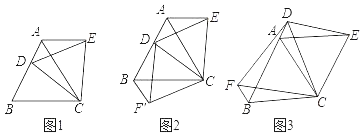
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠1＝∠2，∠C＝∠D。
求证：∠A＝∠F。
证明：∵∠1＝∠2（已知），
又∠1＝∠DMN（_______________），
∴∠2＝∠_________（等量代换），
∴DB∥EC（ ），
∴∠DBC+∠C=1800（两直线平行 , ），
∵∠C＝∠D（ ），
∴∠DBC+ =1800（等量代换），
∴DF∥AC（ ，两直线平行），
∴∠A＝∠F( ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，∠ABC=60°，AB=12cm，将△ABC以点B为中心顺时针旋转，使点C旋转到AB边延长线上的点D处，则AC边扫过的图形（阴影部分）的面积是cm2 ． （结果保留π）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2，将△ABC绕点C按顺时针方向旋转n度后，得到△EDC，此时，点D在AB边上，斜边DE交AC边于点F，则n的大小和图中阴影部分的面积分别为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,直线AB，CD相交于O点，OM⊥AB.
（1）若∠1=∠2，求∠NOD；
（2）若∠1=
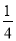∠BOC，求∠AOC与∠MOD.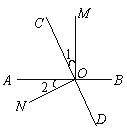 
相关试题
