【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
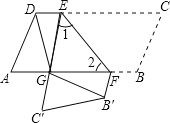
求证:(1)∠1=∠2;
(2)DG=B′G.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据平行四边形得出DC∥AB,推出∠2=∠FEC,由折叠得出∠1=∠FEC=∠2,即可得出答案;
(2)求出EG=B′G,推出∠DEG=∠EGF,由折叠求出∠B′FG=∠EGF,求出DE=B′F,证△DEG≌△B′FG即可.
证明:(1)∵在平行四边形ABCD中,DC∥AB,
∴∠2=∠FEC,
由折叠得:∠1=∠FEC,
∴∠1=∠2;
(2)∵∠1=∠2,
∴EG=GF,
∵AB∥DC,
∴∠DEG=∠EGF,
由折叠得:EC′∥B′F,
∴∠B′FG=∠EGF,
∵DE=BF=B′F,
∴DE=B′F,
∴△DEG≌△B′FG(SAS),
∴DG=B′G.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x-3|和(y-2)2 互为相反数,先化简,并求值(x-2y)2 -(x-y)(x+y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=2,an=3,ap=5,则a2m+n-p的值是( )
A. 2.4 B. 2 C. 1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,
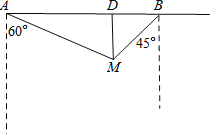
(1)求供水站M到公路AB的垂直距离MD的长度.
(2)求小区A到供水站M的距离.(结果可保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两条边的长分别为2、4,则第三条边的长可以是( )
A. 1 B. 3 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形,是因式分解的是( )
A. 3x(x+y)=3x2+3xy B. -2x2-2xy=-2x(x+y)
C. (x+5)(x-5)=x2-25 D. x2+x+1=x(x+1)+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬“东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
相关试题

