【题目】如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,
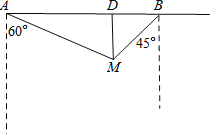
(1)求供水站M到公路AB的垂直距离MD的长度.
(2)求小区A到供水站M的距离.(结果可保留根号)
参考答案:
【答案】(1)150![]() (米);(2)300
(米);(2)300![]() (米).
(米).
【解析】
试题分析:(1)根据题意,在△ABM中,∠BAM=30°,∠ABM=45°,BM=300(![]() +l)米.通过解直角Rt△MBD求得MD的长度;
+l)米.通过解直角Rt△MBD求得MD的长度;
(2)通过解直角Rt△ADM求得AM的长度.
解:由题意可知∠MBD=45°,∠MAD=30°.
(1)在Rt△MBD中,DM=BMsin∠DBM=300×sin45°=150![]() (米);
(米);
(2)在Rt△ADM中,AM=![]() =
=![]() =300
=300![]() (米).
(米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )

A.2
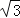 B.4 C.8 D.16
B.4 C.8 D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x-3|和(y-2)2 互为相反数,先化简,并求值(x-2y)2 -(x-y)(x+y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=2,an=3,ap=5,则a2m+n-p的值是( )
A. 2.4 B. 2 C. 1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
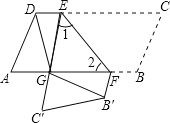
求证:(1)∠1=∠2;
(2)DG=B′G.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两条边的长分别为2、4,则第三条边的长可以是( )
A. 1 B. 3 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形,是因式分解的是( )
A. 3x(x+y)=3x2+3xy B. -2x2-2xy=-2x(x+y)
C. (x+5)(x-5)=x2-25 D. x2+x+1=x(x+1)+1
相关试题

