【题目】已知直线y1=k1x+b1(k1≠0)经过原点和点(-2,-4),直线y2=k2x+b2(k2≠0)经过点(1,5)和点(8,-2).
(1)求y1、y2的函数关系式;
(2)若两条直线相交于点M,求点M的坐标;
(3)若直线y2与x轴交于点N,试求△MON的面积.
参考答案:
【答案】(1) y1=2x,y2=-x+6;(2) M(2,4);(3)12.
【解析】【试题分析】
(1)待定系数法列方程组,可得;
(2)求方程组![]() 的解,即可;
的解,即可;
(3)求出N点坐标再求面积即可.
【试题解析】
(1)已知直线y1=k1x+b1(k1≠0)经过原点和点(-2,-4),
则![]() 解得
解得![]() 所以y1=2x.
所以y1=2x.
已知直线y2=k2x+b2 (k2≠0)经过点(1,5)和点(8,-2),则
![]() 解得
解得![]() 所以y2=-x+6.
所以y2=-x+6.
(2)解方程组![]()
![]() ,得M(2,4).
,得M(2,4).
(3)令y2 =0,解得x=6,即N(6,0),因此![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=
 过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.(1)根据现有的信息,请求出题中的一次函数的解析式.
(2)根据关系式画出这个函数图象.
(3)过点B能不能画出一直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并求出其中一条直线所对应的函数关系式,其它的直接写出函数关系式;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的曲线表示小华星期天骑自行车外出离家的距离与时间的关系,小华八点离开家,十四点回到家,根据这个曲线图,请回答下列问题:
(1)到达离家最远的地方是几点?离家多远?
(2)何时开始第一次休息?休息多长时间?
(3)小华在往返全程中,在什么时间范围内平均速度最快?最快速度是多少?
(4)小华何时离家21千米?(写出计算过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物小组观察一植物生长,得到植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行x轴).
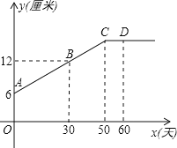
(1)该植物从观察时起,多少天以后停止长高?
(2)求直线AC的解析式,并求该植物最高长多少厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 经过一点有且只有一条直线与已知直线平行
B. 直线外一点到这条直线的垂线段,叫做点到直线的距离
C. 同一平面内,不相交的两条直线是平行线
D. “相等的角是对顶角”是真命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算6×(7+1)×(72+1)×(74+1)×(78+1)+1的个位数字为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,属于真命题的是( )
A. 同位角互补B. 多边形的外角和小于内角和
C. 平方根等于本身的数是1D. 同一平面内,垂直于同一条直线的两条直线平行
相关试题

