【题目】如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为36,则PD+PE+PF=( )
A.12
B.8
C.4
D.3
参考答案:
【答案】A
【解析】解:如图,延长EP、FP分别交AB、BC于G、H,则由PD∥AB,PE∥BC,PF∥AC,
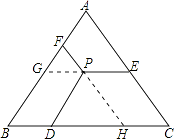
∴四边形PGBD和四边形EPHC是平行四边形,
∴PG=BD,PE=HC,
又△ABC是等边三角形,
又有PF∥AC,PD∥AB可得△PFG,△PDH是等边三角形,
∴PF=PG=BD,PD=DH,
又△ABC的周长为36,
∴PD+PE+PF=DH+HC+BD=BC= ![]() ×36=12,
×36=12,
故A符合题意.
故答案为:A.
延长EP、FP分别交AB、BC于G、H,易证得四边形PGBD、四边形EPHC是平行四边形以及△PFG、△PDH是等边三角形,进而根据三角形的周长可求得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A=
 ÷(a﹣
÷(a﹣ ).
).(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);…解关于x的不等式:
 ≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QO,设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
②在如图中,若∠A=30
 ,∠C=70
,∠C=70 ,则∠P的度数为__ _;
,则∠P的度数为__ _;(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
-
科目: 来源: 题型:
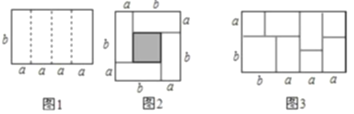
查看答案和解析>>【题目】如图是一个长为
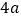 、宽为
、宽为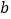 的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).(1)如图中的阴影部分面积为: ;(用
 、
、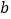 的代数式表示)
的代数式表示)(2)观察如图,请你写出
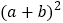 、
、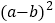 、
、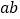 之间的等量关系是 ;
之间的等量关系是 ;(3)根据(2)中的结论,若
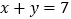 ,
,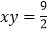 ,则
,则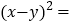 ;
;(4)实际上通过计算图形的阴影可以探求相应的等式,如图,请你写出这个等式 ;
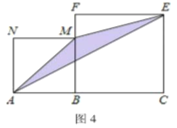
(5)如图,线段
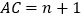 (其中
(其中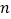 为正数),点
为正数),点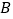 线在段
线在段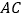 上,在线段
上,在线段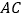 同侧作正方形
同侧作正方形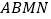 及正方形
及正方形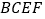 ,连接
,连接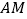 ,
,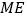 ,
, 得到
得到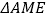 .当
.当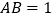 时,
时,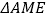 的面积记为
的面积记为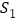 ;当
;当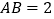 时,
时,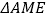 的面积记为
的面积记为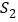 ;当
;当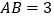 时,
时,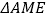 的面积记为
的面积记为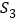 ;当
;当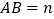 时,
时,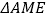 的面积记为
的面积记为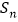 ,则
,则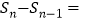 .
.
相关试题

