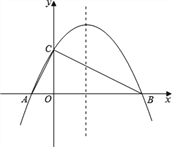
【题目】如图,已知抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(﹣2,0).
与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式;
(2)求△ABC的外接圆圆心坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2) 圆心坐标为(3,0);(3)见解析.
;(2) 圆心坐标为(3,0);(3)见解析.
【解析】分析:
(1)将A、C两点的坐标代入抛物线的解析式列出关于b、c的方程组,解方程组求得b、c的值即可得到所求解析式;
(2)由(1)中所得解析式先求出点B的坐标,再结合点A、C的坐标求得线段AC、BC、AB的长,由勾股定理的逆定理证得∠ACB=90°,由此即可得到△ABC的外心是斜边AB的中点,由此即可得到所求坐标;
(3)由(1)中所得抛物线的解析式可求得抛物线的对称轴为直线x=3,设点Q的坐标为(3,t),结合点A、C的坐标可将AC、AQ和CQ的长度表达出来,然后分AQ=CQ、AC=CQ和AQ=AC三种情况列出方程,解方程即可求得符合条件的点Q的坐标.
详解:
(1)∵抛物线![]() 的图象经过点A(﹣2,0),C(0,4)
的图象经过点A(﹣2,0),C(0,4)
∴ 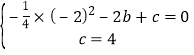
解得:b=![]() ,c=4
,c=4
∴抛物线解析式为![]() ;
;
(2)在![]() 中,令y=0,即
中,令y=0,即![]() ,
,
整理得x2﹣6x﹣16=0,解得:x=8或x=﹣2,
∴A(﹣2,0),B(8,0),
∴OA=2,OC=4,OB=8,AB=10,
∴![]()
![]()
![]() ,
,
∴![]()
∴△ABC是直角三角形,且![]() ,
,
∴△ABC的外接圆圆心在AB边上的中点处,圆心坐标为(3,0),

(3)∵![]() ,
,
∴抛物线的线的对称轴为:x=3,
可设点Q(3,t),∵点A、C的坐标分别为(-2,0)和(0,4),
∴AC=![]() ,AQ=
,AQ=![]() ,CQ=
,CQ=![]() ,
,
i)当AQ=CQ时,
有![]() ,即25+t2=t2﹣8t+16+9,
,即25+t2=t2﹣8t+16+9,
解得t=0,
∴Q1(3,0);
ii)当AC=AQ时,
有![]() ,即
,即![]() ,此方程无实数根,
,此方程无实数根,
∴此时△ACQ不能构成等腰三角形;
iii)当AC=CQ时,
有![]() ,即:t2﹣8t+5=0,
,即:t2﹣8t+5=0,
解得:t=4±![]() ,
,
∴点Q坐标为:Q2(3,4+![]() ),Q3(3,4﹣
),Q3(3,4﹣![]() ).
).
综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+![]() ),Q3(3,4﹣
),Q3(3,4﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+
 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+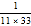 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目
测试成绩/分
甲
乙
丙
笔试
92
90
95
面试
85
95
80
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
-
科目: 来源: 题型:
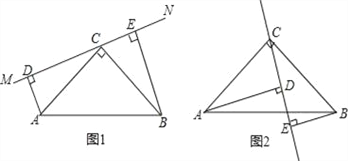
查看答案和解析>>【题目】如图(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.求证:
(1)△ADC≌△CEB;
(2)DE=AD+BE.
(3)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE又怎样的关系?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-2x+2的图象与
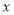 轴、
轴、 轴分别交于点
轴分别交于点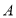 、
、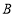 ,以线段
,以线段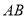 为直角边在第一象限内作等腰直角三角形ABC,且
为直角边在第一象限内作等腰直角三角形ABC,且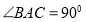 ,则点C坐标为_____.
,则点C坐标为_____.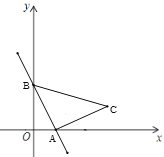
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(1)①∠BCE与∠CDF的大小关系是_______________;
②证明:GF⊥BF;
(2)探究G落在边DC的什么位置时,BF=BC,请说明理由.

相关试题

