【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
参考答案:
【答案】(1)155°;(2)OE平分∠BOC.
【解析】
(1)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;
(2)根据∠COE=∠DOE﹣∠DOC和∠BOE=∠BOD﹣∠DOE分别求得∠COE与∠BOE的度数即可说明.
解:(1)因为∠AOC=50°,OD平分∠AOC,
所以∠DOC=![]() ∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
所以∠BOD=∠DOC+∠BOC=155°;
(2)OE平分∠BOC.理由如下:
因为∠DOE=90°,∠DOC=25°,
所以∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.
又因为∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,
所以∠COE=∠BOE,
所以OE平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如:
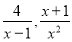 。当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:
。当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如: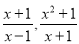 。假分式可以化为整式与真分式和的形式,我们也称之为带分式,如:
。假分式可以化为整式与真分式和的形式,我们也称之为带分式,如: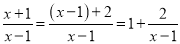 。
。解决问题:
(1)下列分式中属于真分式的是( )
A.
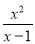 B.
B.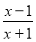 C.
C.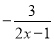 D.
D.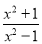
(2)将假分式
 分别化为带分式;
分别化为带分式;(3)若假分式
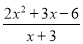 的值为整数,请直接写出所有符合条件的整数x的值。
的值为整数,请直接写出所有符合条件的整数x的值。 -
科目: 来源: 题型:
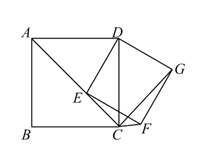
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG。
(1)求证:矩形DEFG是正方形。
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)所有的等腰三角形都相似;(2)所有的等腰直角三角形都相似;(3)有一个角相等的两个等腰三角形相似(4)顶角相等的两个等腰三角形相似.
其中正确的有( )
A.
 个B.
个B.  个C.
个C.  个D.
个D. 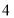 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=
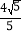 ;④AF=
;④AF=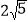 ,其中正确的是______.(填写所有正确结论的序号)
,其中正确的是______.(填写所有正确结论的序号)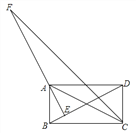
-
科目: 来源: 题型:
查看答案和解析>>【题目】美是一种感觉,本应没有什么客观的标准,但在自然界里,物体形状的比例却提供了在的称与协调上的一种美感的参考,在数学上,这个比例称为黄金分割.在人体由脚底至肚脐的长度与身高的比例上,肚脐是理想的黄金分割点,也就是说,若此比值越接近
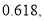 就越给别人一种美的感觉. 某女士身高为
就越给别人一种美的感觉. 某女士身高为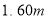 ,脚底至肚脐的长度与身高的比为
,脚底至肚脐的长度与身高的比为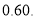 为了追求美,地想利用高跟鞋达到这一效果 ,那么她选的高跟鞋的高度约为( )
为了追求美,地想利用高跟鞋达到这一效果 ,那么她选的高跟鞋的高度约为( )A.
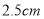 B.
B. 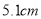 C.
C. 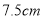 D.
D. 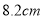
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知图甲是一个长为
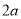 ,宽为
,宽为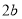 的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.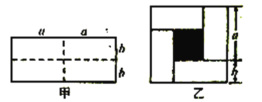
(1)求图乙中阴影部分正方形的边长(用含字母
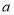 ,
,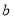 的整式表示);
的整式表示);(2)请用两种不同的方法求图乙中阴影部分的面积.
(3)观察图乙,并结合(2)中的结论,写出下列三个整式:
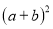 ,
,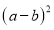 ,
,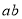 之间的等量关系;
之间的等量关系;(4)根据(3)题中的等量关系,解决如下问题:若
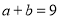 ,
,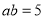 ,求
,求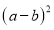 的值.
的值.
相关试题

