【题目】实践操作:如图,在 ![]() 中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
(1)作∠BCA的角平分线,交AB于点O;
(2)以O为圆心,OB为半径作圆.
综合运用:在你所作的图中,
(3)AC与⊙O的位置关系是(直接写出答案);
(4)若BC=6,AB=8,求⊙O的半径.
参考答案:
【答案】
(1)解:如图所示:CO即为所求;
(2)解:如图所示:⊙O即为所求;
(3)解:相切
(4)解:过点O连接AC与⊙O的切点E,
∵BC=6,AB=8,∠ABC=90°,
∴AC=10,
∵CB是⊙O的切线,切点为B,
∴CE=CB=6,
又∵AC=AE+CE,
∴AE=AC-CE=10-6=4,
设BO=x,则EO=x,AO=6-x,
在Rt△AOE中,
AE2+EO2=AO2 ,
即42+x2=(8-x)2 ,
解得:x=3,
∴⊙O的半径为3。
【解析】(3)过圆心向直线引垂线,证明垂线段等与圆的半径;(4)利用勾股定理,设出半径建立方程,解方程,求出半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,是一个长为
 ,宽为
,宽为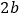 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。(1)你认为图2中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法求图2中阴影部分的面积.
方法1 ;方法2 ;
(3)仔细观察图2,写出
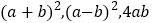 三个代数式之间的等量关系.
三个代数式之间的等量关系.(4)若
 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于雾霾天气对人们健康的影响,市场上的空气净化器成了热销产品.某公司经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=-2x+1000.
(1)该公司每月的利润为w元,写出利润w与销售单价x的函数关系式;
(2)若要使每月的利润为40000元,销售单价应定为多少元?
(3)公司要求销售单价不低于250元,也不高于400元,求该公司每月的最高利润和最低利润分别为多少? -
科目: 来源: 题型:
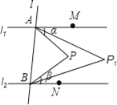
查看答案和解析>>【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____ km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
(4)图中A点表示___________________________________;
(5)小明从中心书城到滨海公园的平均速度为______km/h,小明爸爸驾车的平均速度为______km/h;(补充;爸爸驾车经过______追上小明);
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形的斜边
 在
在 轴的正半轴上,点
轴的正半轴上,点 与原点重合,点
与原点重合,点 的坐标是
的坐标是 ,且
,且 ,若将
,若将 绕着点
绕着点 旋转后30°,点
旋转后30°,点 和
和 点分别落在点
点分别落在点 和点
和点 处,那么直线
处,那么直线 的解析式是__________.
的解析式是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】节能灯在城市已基本普及,今年某省面向县级及农村地区推广,为相应号召,某商场计划用3800元购进节能灯120只,这两种节能灯的进价、售价如下表:
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?

相关试题

