【题目】如图,四边形ABCD是矩形,![]() ,
,![]() ,点P是对角线AC上的动点
,点P是对角线AC上的动点![]() 不与点A,C重合
不与点A,C重合![]() ,连接PD,作
,连接PD,作![]() 交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.
交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.

![]() 线段PD的最小值为______;
线段PD的最小值为______;
![]() 求证:
求证:![]() ,并求矩形PEFD面积的最小值;
,并求矩形PEFD面积的最小值;
![]() 是否存在这样的点P,使得
是否存在这样的点P,使得![]() 是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3) PE的长为
;(2)证明见解析;(3) PE的长为![]() 或
或![]() .
.
【解析】
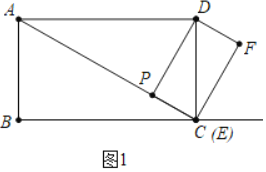
![]() 如图1中,根据垂线段最短可知,当
如图1中,根据垂线段最短可知,当![]() 时,DP的值最小
时,DP的值最小![]() 利用面积法即可解决问题;
利用面积法即可解决问题;
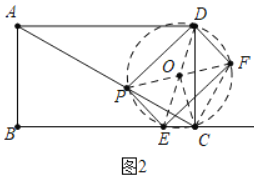
![]() 如图2中,连接DE、PF交于点O,连接FC,
如图2中,连接DE、PF交于点O,连接FC,![]() 首先证明D、P、E、C、F五点共圆,由
首先证明D、P、E、C、F五点共圆,由![]() ∽
∽![]() ,推出
,推出![]() ,即可解决问题;
,即可解决问题;
![]() 分两种情形:点E在线段BC上,点E在线段BC的延长线上,分别求解即可解决问题;
分两种情形:点E在线段BC上,点E在线段BC的延长线上,分别求解即可解决问题;
![]() 解:如图1中,根据垂线段最短可知,当
解:如图1中,根据垂线段最短可知,当![]() 时,DP的值最小.
时,DP的值最小.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案为![]() .
.
![]() 证明:如图2中,连接DE、PF交于点O,连接FC,OC.
证明:如图2中,连接DE、PF交于点O,连接FC,OC.
![]() 四边形DPEF是矩形,
四边形DPEF是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 、P、E、C、F五点共圆,
、P、E、C、F五点共圆,
![]() 是直径,
是直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∴S矩形PEFD=PE·PD=![]() PD2.
PD2.
∵PD的最小值是![]() ,
,
∴矩形PEFD面积的最小值是=![]() ×(
×(![]() )2=
)2=![]() .
.
![]() 解:如图3中,设AC交DE于H.
解:如图3中,设AC交DE于H.
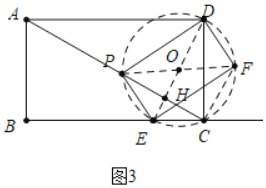
当![]() 时,易证
时,易证![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
如图4中,
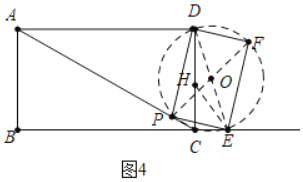
当![]() 时,
时,![]() ,
,
![]() ,
,
在CD上取一点H,速度![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
综上所述,PE的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
: .
. 求抛物线
求抛物线 的对称轴;
的对称轴; 无论a为何值,抛物线
无论a为何值,抛物线 都经过两个定点,求这两个定点的坐标;
都经过两个定点,求这两个定点的坐标; 将抛物线
将抛物线 沿
沿 中两个定点所在直线翻折,得到抛物线
中两个定点所在直线翻折,得到抛物线 ,当
,当 的顶点到x轴的距离为1时,求抛物线
的顶点到x轴的距离为1时,求抛物线 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么,按照图中所标注的数据,图中实线所围成的图形面积为( ).

A.40.5B.48.5C.50D.52.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D,E为BC边上的两点,且∠DAE=45°,连接EF,BF,则下列结论:①△AFB≌△ADC;②△ABD为等腰三角形;③∠ADC=120°;④BE2+DC2=DE2,其中正确的有( )个

A.4B.3C.2D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 三边的中线 AD,BE,CF 相交于点 G,若 S△ABC=15,则图中阴影部分面积是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,则AC=______,AB=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm.则△ADE的周长________.

相关试题

