【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D,E为BC边上的两点,且∠DAE=45°,连接EF,BF,则下列结论:①△AFB≌△ADC;②△ABD为等腰三角形;③∠ADC=120°;④BE2+DC2=DE2,其中正确的有( )个

A.4B.3C.2D.1
参考答案:
【答案】C
【解析】
根据∠DAF=∠BAC=90°,可以得出∠FAB=∠DAC,利用SAS可证△AFB≌△ADC,所以,可判断①正确;没有条件可以证得△ABD为等腰三角形与∠ADC=120°;根据∠DAF=90°,∠DAE=45°,可以得出∠FAE=45°,再利用SAS证明△AED≌△AED,得到EF=ED,由①可知BF=CD,∠FBA=∠C=45°,从而可以证得∠FBE=90°,得到BE2+DC2=DE2.
①因为∠DAF=∠BAC=90°,即∠FAB+∠BAD=∠BAD+∠DAC,所以∠FAB=∠DAC,在△AFB≌△ADC中,AF=AD,∠FAB=∠DAC,AB=AC,所以△AFB≌△ADC,所以①正确;
②在Rt△ABC中,AB=AC,可以得出∠ABC=∠C=45°,但D、是BC上的点,所以AD一定不等于AB,所以②错误;
③没有任何条件可以证出∠ADC=120°,所以③错误;
④由①可知BF=CD,∠FBA=∠C=45°,所以∠FBA+∠ABC=90°,即∠FBE=90°,根据勾股定理可知![]() ,所以BE2+DC2=DE2成立,所以④正确;
,所以BE2+DC2=DE2成立,所以④正确;
综上所述,答案选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者
 根据国家信息中心发布的
根据国家信息中心发布的 中国分享经济发展报告
中国分享经济发展报告 显示,2016年我国共享经济市场交易额约为34520亿元,比上年增长
显示,2016年我国共享经济市场交易额约为34520亿元,比上年增长 ;超6亿人参与共享经济活动,比上年增加约1亿人.
;超6亿人参与共享经济活动,比上年增加约1亿人.小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为A,B,C,D的四张卡片
 除编号和内容外,其余完全相同
除编号和内容外,其余完全相同 他们将这四张卡片背面朝上,洗匀放好.
他们将这四张卡片背面朝上,洗匀放好.
 从中随机抽取一张,恰好抽到“共享服务”的概率是______.
从中随机抽取一张,恰好抽到“共享服务”的概率是______. 从中随机抽取一张
从中随机抽取一张 不放回
不放回 ,再从中随机抽取一张请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率
,再从中随机抽取一张请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率 这四张卡片分别用它们的编号A,B,C,D表示
这四张卡片分别用它们的编号A,B,C,D表示 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
: .
. 求抛物线
求抛物线 的对称轴;
的对称轴; 无论a为何值,抛物线
无论a为何值,抛物线 都经过两个定点,求这两个定点的坐标;
都经过两个定点,求这两个定点的坐标; 将抛物线
将抛物线 沿
沿 中两个定点所在直线翻折,得到抛物线
中两个定点所在直线翻折,得到抛物线 ,当
,当 的顶点到x轴的距离为1时,求抛物线
的顶点到x轴的距离为1时,求抛物线 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么,按照图中所标注的数据,图中实线所围成的图形面积为( ).

A.40.5B.48.5C.50D.52.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,
 ,
, ,点P是对角线AC上的动点
,点P是对角线AC上的动点 不与点A,C重合
不与点A,C重合 ,连接PD,作
,连接PD,作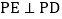 交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.
交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.
 线段PD的最小值为______;
线段PD的最小值为______; 求证:
求证: ,并求矩形PEFD面积的最小值;
,并求矩形PEFD面积的最小值; 是否存在这样的点P,使得
是否存在这样的点P,使得 是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 三边的中线 AD,BE,CF 相交于点 G,若 S△ABC=15,则图中阴影部分面积是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,则AC=______,AB=________.

相关试题

