【题目】如图,在Rt△ABC中,∠B=Rt∠,直角边AB、BC的长(AB<BC)是方程 ![]() 2-7
2-7 ![]() +12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).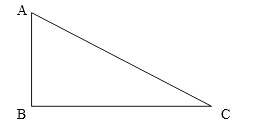
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为 ![]() 时运动时间t的值;
时运动时间t的值;
(3)点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
∵x2-7x+12=(x-3)(x-4)=0 ∴x1=3或x2=4.则AB=3,BC=4.
(2)
由题意得AB2+BP2=AP2,则32+(t-3)2=10,
解得t1=4,t2=2(舍).
即t=4时,AP=![]() .
.
(3)
存在点P,使△ABP是等腰三角形.
①当AP=AB=3时,P在CC,则 t=3+4+5-3=9(秒).
②当BP=BA=3时,当P在AC上时, t=![]() (秒),
(秒),
当P在BC上时, t=3+3=6 (秒),
③当BP=AP (即P为AC中点)时, ∴t=3+4+2.5=9.5(秒).
可知当t为9秒或9.5秒或6 (秒)或![]() (秒)时,△ABP是等腰三角形.
(秒)时,△ABP是等腰三角形.
【解析】(1)运用因式分解法求;
(2)由勾股定理构造方程,解出t的值;
(3)分类讨论:①当AP=AB=3时,②当BP=BA=3时,③当BP=AP.
【考点精析】通过灵活运用因式分解法和等腰三角形的性质,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=-x2+2x+n图象的顶点坐标是(m,1),则m-n的值为( )
A.1B.0C.1D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口约为44亿人,数据44亿用科学记数法表示为( )
A. 44×108 B. 4.4×109 C. 4.4×108 D. 44×1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程ax2+3x=ax+2是一元二次方程,那么( )
A.a≠0B.a≠1C.a≠2D.a≠3
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校初一某班学生的平均体重是45公斤.
(1)下表给出了该班6位同学的体重情况(单位:公斤),完成下表
姓 名
小丽
小华
小明
小方
小颖
小宝
体 重
37
50
40
36
48
体重与平均体重的差值
﹣8
+5
+2
(2)最重的与最轻的同学的体重相差多少?
(3)这6位同学的平均体重是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )
A.赚16元
B.赔16元
C.不赚不赔
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)如图,在平面直角坐标系中,抛物线
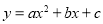 与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在
与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在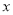 轴上且AD为⊙M的直径.点E是⊙M与
轴上且AD为⊙M的直径.点E是⊙M与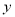 轴的另一个交点,过劣弧
轴的另一个交点,过劣弧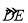 上的点F作FH⊥AD于点H,且FH=1.5.
上的点F作FH⊥AD于点H,且FH=1.5.
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是
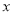 轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使⊿QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
相关试题

