【题目】将正整数1至2019按照一定规律排成下表:

记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a42=_________, a53=_________;
(2)①如果aij=2019,那么i=_________, j =_________;②用i,j表示aij=_____________;
(3) 将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027.若能,求出这5个数中的最小数,若不能说明理由。
参考答案:
【答案】26; 35; 253 3 aij=8(i-1) + j
(3)不能等于2027,理由见解析
【解析】
(1) 观察表格中的数据,根据数据的变化可求出a4, a53的值;
(2)①根据数据的变化,找出2019所在的位置;②由数的变化,找出aij的值;
(3)设这5个数中的最小数为x,则其余4个数可表示为x+4, x+9, x+11, x+18,由5个数之和为2027可得出关于x的一元-次方程,解之即可得出x的值,再找出x,(x+4) 所在的位置,由这两个数不在同一行可得出所覆盖的5个数之和不能等于2027.
解:(1)∵前面3行一共有![]() 个数,
个数,
∴第4行的第1个数为25,则第4行的第2个数为26,即![]() ;
;
∵前面4行一 共有![]() 个数,
个数,
∴第5行的第1个数为33,则第5行的第3个数为35,即![]() .
.
故答案为: 26; 35.
(2)①∵![]() ,
,
∴2019是第253行的第3个数,
∴i=253, j=3.
故答案为: 253; 3.
②根据题意得:![]() .
.
故答案为8 (i-1) +j.
(3)设这5个数中的最小数为x,则其余4个数可表示为x+4, x+9, x+11, x +18,
根据题意得:x+x+4+x+9+x+11 +x+ 18=2027,
解得x=397.
∵397=49×8+5,
∴397是第50行的第5个数,
而此时x+4=401是第51行的第1个数,与397不在同一行,
∴将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和不能等于2027.
-
科目: 来源: 题型:
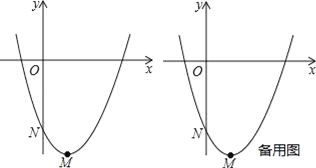
查看答案和解析>>【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD交于点O,将一个三角板的直角顶点放置于O处,使其两条直角边分别位于OC的两侧,若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,点
中,点 在边
在边 上,联结
上,联结 .
. 如图,将
如图,将 沿着
沿着 翻折,点
翻折,点 的对应点是点
的对应点是点 ,若
,若 平分
平分 ,则
,则 的值等于 ;
的值等于 ;
 若
若 .将
.将 绕着点
绕着点 旋转,使得点
旋转,使得点 的对应点
的对应点 落在边
落在边 上,点
上,点 的对应点分别是点
的对应点分别是点 ,则
,则 的面积等于 .
的面积等于 . -
科目: 来源: 题型:
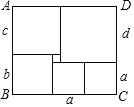
查看答案和解析>>【题目】如图,长方形ABCD被分成六个小的正方,已知中间一个小正方形的边长为1,其它正方形的边长分别为a、b、c、d.观察图形并探索:(1)b=_____,d=_____;(用含a的代数式表示)(2)长方形ABCD的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:
①CF=AE;②OE=OF;③图中共有四对全等三角形;④四边形ABCD是平行四边形;其中正确结论的是_____________________.

相关试题

