搜索
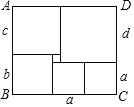
【题目】如图，长方形ABCD被分成六个小的正方，已知中间一个小正方形的边长为1，其它正方形的边长分别为a、b、c、d．观察图形并探索：（1）b＝_____，d＝_____；（用含a的代数式表示）（2）长方形ABCD的面积为_____．
参考答案：
【答案】a+1 2a﹣1 143
【解析】
（1）利用中间一个小正方形的边长为1，得出b，d与a的关系；
（2）利用c＝b+1，b＝a+1，得出c＝a+2，再利用c＝d﹣1，d＝2a﹣1，得出c＝2a﹣2，那么2a﹣2＝a+2，解方程求出a的值，然后分别计算出长方形ABCD的长与宽，进而求出面积．
（1）∵中间一个小正方形的边长为1，
∴b＝a+1，d＝2a﹣1；
故答案为：a+1，2a﹣1；
（2）∵c＝b+1，b＝a+1，
∴c＝a+2，
又∵c＝d﹣1，d＝2a﹣1，
∴c＝2a﹣2，
∴2a﹣2＝a+2，
解得a＝4．
则长方形ABCD的长为c+d＝a+2+2a﹣1＝3a+1＝13，
宽为a+d＝a+2a﹣1＝3a﹣1＝11，
所以长方形ABCD的面积为：11×13＝143．
故答案为：143．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB、CD交于点O，将一个三角板的直角顶点放置于O处，使其两条直角边分别位于OC的两侧，若OC刚好平分∠BOF，∠BOE=2∠COE，求∠BOD的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将正整数1至2019按照一定规律排成下表：
记aij表示第i行第j个数，如a14=4表示第1行第4个数是4.
（1）直接写出a42=_________， a53=_________；
（2）①如果aij=2019，那么i=_________， j =_________；②用i，j表示aij=_____________；
（3） 将表格中的5个阴影格子看成一个整体并平移，所覆盖的5个数之和能否等于2027.若能，求出这5个数中的最小数，若不能说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】在
中，点
在边
上，联结
.
如图，将
沿着
翻折，点
的对应点是点
，若
平分
，则
的值等于 ；
若
.将绕着点旋转，使得点
的对应点
落在边上，点
的对应点分别是点
，则
的面积等于 . -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE，若DE=BF，则下列结论：
①CF=AE；②OE=OF；③图中共有四对全等三角形；④四边形ABCD是平行四边形；其中正确结论的是_____________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，以对角线BD为一边构造一个矩形BDEF，使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1，Rt△BFC的面积为S2，Rt△DCE的面积为S3，则S1__ __S2＋S3；(填“＞”“＝”或“＜”)
(2)写出图中的三对相似三角形，并选择其中一对进行证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】
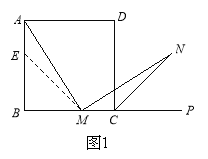
（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．
（下面请你完成余下的证明过程）
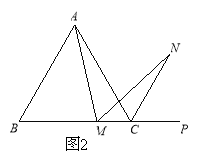
（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正
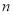边形ABCD……X”，请你作出猜想：当∠AMN= °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）
相关试题
