搜索
【题目】如图，在△ABC中，点D，E分别是AB，C的中点，则S△ADE：S△ABC=（ ）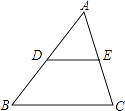 
A.1：2
B.1：3
C.1：4
D.1：5
参考答案：
【答案】C
【解析】解：∵点D、E分别是AB、C的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE= 
BC，
∴△ADE∽△ABC，
∴S△ADE：S△ABC=（ ）2= 
；
故选：C．
【考点精析】关于本题考查的三角形中位线定理和相似三角形的判定与性质，需要了解连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将两条宽度都为3的纸条重叠在一起，使∠ABC=60°，则四边形ABCD的面积为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：a＝
，
，c是-27的立方根.（1）b ＝_______，c ＝_______；
（2）化简a，并求a+b-c的平方根；
（3）若关于
的不等式组
无解，求
的取值范围. -
科目： 来源： 题型：
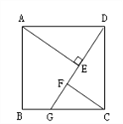
查看答案和解析>>【题目】四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F.
（1） 在图中找出一对全等三角形，并加以证明；
（2）求证：AE=FC+EF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC，BD相交于点O，AC平分∠DCB，CD⊥AD，∠ACD＝45°，∠BAC＝60°.
（1）证明：AD∥BC；
（2）求∠EAD的度数；
（3）求证：∠AOB＝∠DAC +∠CBD
-
科目： 来源： 题型：
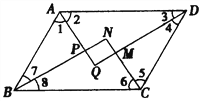
查看答案和解析>>【题目】如图，□ABCD中，AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线，AQ与BN交于P，CN与DQ交于M，在不添加其它条件的情况下，试写出一个由上述条件推出的结论，并给出证明过程（要求：推理过程中要用到“平行四边形”和“角平分线”这两个条件）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在2×2的正方形网格中有9个格点，已经取定点A，B，C，在余下的6个点中任取一点P，满足△ABP与△ABC相似的概率是（ ）
A.
B.
C.
D.
相关试题
