【题目】如图,D是△ABC的BC边上的一点,∠B =40°,∠ADC=80°.
(1)求证:AD=BD;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)△ABC是等腰三角形,理由见解析.
【解析】试题分析:(1)由由三角形外角的性质,可求得∠BAD的度数,根据等角对等边,可得AD=BD;
(2)由∠BAC=70°,易求得∠C=∠BAC=70°,根据等角对等边的性质,可证得△ABC是等腰三角形.
(1)∵∠ADC=∠B+∠BAD,而∠ADC=80°,∠B =40°,
∴∠BAD=80°-40°=40°,
∴∠B=∠BAD,
∴AD=BD.
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,
∴∠C=180°﹣∠B﹣∠BAC=70°,
∴∠C=∠BAC,
∴BA=BC,
∴△ABC是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据条件,求下列代数式的值:
(1)若
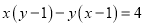 ,求
,求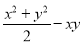 的值。
的值。(2)若
 求代数式
求代数式 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2017秒时,点P的坐标是( )
个单位长度,则第2017秒时,点P的坐标是( )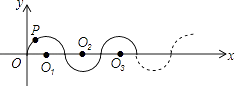
A.(2016,0)
B.(2017,1)
C.(2017,﹣1)
D.(2018,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
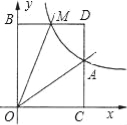
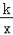 的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.(1)求反比例函数的解析式;
(2)当∠OAM=90°时,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强居民的节电意识,某城区电价执“阶梯式”计费,每月应交电费y(元)与用电量x(度)之间的函数关系如图所示,请写出每月应交电费与用电量的函数关系式;若某用户12月份交电费68元,求该用户12月份的用电量.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家体育馆“鸟巢”的建筑面积达25.8万平方米,请将“25.8万”用科学记数法表示,结果是( )
A.25.8×104
B.25.8×105
C.2.58×104
D.2.58×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于实数a,符号[a]表示不大于a的最大整数,例如:[4.7]=4,[﹣π]=﹣4,[3]=3,如果[
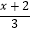 +1]=﹣5,则x的取值范围为 .
+1]=﹣5,则x的取值范围为 .
相关试题

