【题目】如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )

A.60° B.65° C.55° D.50°
参考答案:
【答案】A
【解析】
试题分析:根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.
解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=540°﹣300°=240°,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠PDC+∠PCD=![]() (∠BCD+∠CDE)=120°,
(∠BCD+∠CDE)=120°,
∴∠P=180°﹣120°=60°.
故选:A.
-
科目: 来源: 题型:
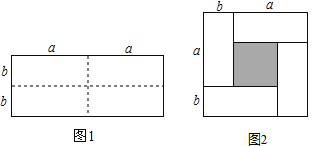
查看答案和解析>>【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a﹣b)2,(a+b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=4,ab=3.求代数式a﹣b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由若干个完全相同的小正方体堆成的一个几何体放置在平整的地面上.
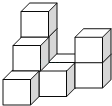
(1)请画出这个几何体的三视图.
(2)如果在这个几何体的表面喷上红色的漆,则在所有的小正方体中,有 个小正方体只有一个面是红色,有 个小正方体只有两个面是红色,有 个小正方体只有三个面是红色.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,﹣3)关于x轴的对称点是__________,关于y轴的对称点是__________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣24+3×(﹣1)2016+100÷(﹣5)2
(2)
 xy﹣
xy﹣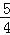 x2y2﹣
x2y2﹣ xy2+
xy2+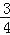 xy﹣
xy﹣ xy2
xy2(3)4y2﹣[3y﹣(3﹣2y)+2y2]﹣2
(4)
 xy﹣
xy﹣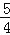 x2y2﹣
x2y2﹣ xy2+
xy2+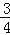 xy﹣
xy﹣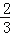 xy2.
xy2. -
科目: 来源: 题型:
查看答案和解析>>【题目】五水共治检查组从A市到B市有一天的路程,计划上午比下午多走100千米到C市吃午饭.由于堵车,中午才赶到一个小镇,只行驶了原计划的三分之一,过了小镇,汽车赶了400千米才停下来休息.司机说:“再走从C市到这里路程的二分之一就到达目的地了”.则A市到B市的路程为( )
A.600千米 B.700千米 C.800千米 D.1200千米
-
科目: 来源: 题型:
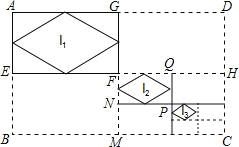
查看答案和解析>>【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是 cm2.
相关试题

