Question

【题目】我国是世界上严重缺水的国家之一，2011年春季以来，我省遭受了严重的旱情，某校为了组织“节约用水从我做起”活动，随机调查了本校120名同学家庭月人均用水量和节水措施情况，如图1、图2是根据调查结果做出的统计图的一部分．

请根据信息解答下列问题：

(1)图1中淘米水浇花所占的百分比为 ；

(2)图1中安装节水设备所在的扇形的圆心角度数为 ；

(3)补全图2；

(4)如果全校学生家庭总人数为3000人，根据这120名同学家庭月人均用水量，估计全校学生家庭月用水总量是多少吨？

Answer 1

【答案】【解】 (1)15﹪；(2)108°；(3) 见解析；(4)全校学生家庭月用水总量是9600吨

【解析】

（1）根据扇形统计图的特点可知，用1减去其他3种节水措施所占的百分比即可解答．
（2）用安装节水设备所在的扇形的百分比乘360度，即可得出正确答案．
（3）根据随机调查了本校120名同学家庭可知总数为120，减去其他4组的户数得出答案，再画图即可解答．
（4）先求出这120名同学家庭月人均用水量，再用样本估计总体的方法即可解答．

（1）淘米水浇花所占的百分比为1-30%-44%-11%=15%．
（2）安装节水设备所在的扇形的圆心角度数为360°×30%=108°．
（3）如图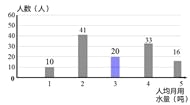

（4）（1×10+2×42+3×20+4×32+5×16）÷120×3000
=9100吨．
即全校学生家庭月用水总量是9100吨．