Question

【题目】如图，△ABC和△ADE都是等腰三角形，BC、DE分别是这两个等腰三角形的底边，且∠BAC=∠DAE．

（1）求证：BD=CE；

（2）连接DC．如果CD=CE，试说明直线AD垂直平分线段BC．

Answer 1

【答案】(1)证明见解析；（2）说明见解析.

【解析】（1）由△ABC和△ADE都是等腰三角形且∠BAC=∠DAE知AB=AC、AD=AE、∠BAD=∠CAE，证△ABD≌△ACE即可得证；

（2）由（1）知BD=CE，结合CD=CE知CD=BD，据此可得点D在BC的中垂线上，根据AB=AC知点A在BC的中垂线上，从而得出AD垂直平分线段BC．

（1）∵△ABC和△ADE都是等腰三角形，且∠BAC=∠DAE，∴AB=AC，AD=AE，∠BAD=∠CAE．

在△ABD和△ACE中，

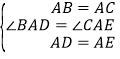∵，∴△ABD≌△ACE（SAS），∴BD=CE．

（2）由（1）知△ABD≌△ACE，∴BD=CE．

∵CD=CE，∴CD=BD，∴点D在BC的中垂线上．

∵AB=AC，∴点A在BC的中垂线上，∴AD垂直平分线段BC．