【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由四边形ABCD是平行四边形,CE=DC,易证得∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,则可证得△ABF≌△ECF;
(2)由△ABF≌△ECF,∠AFC=2∠ABC,即可证得∠ABC=∠BAF,继而证得AE=BC,又由AD=BC,则可得AE=AD,再利用等腰三角形三线合一的性质可得AC⊥ED,进而可得结论.
试题解析:证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵EC=DC,
∴AB=EC,
在△ABF和△ECF中,
∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,
∴△ABF≌△ECF(AAS);
(2)∵△ABF≌△ECF,
∴AF=FE,BF=FC.
∵∠AFC=2∠ABC,
又∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF.
∴AF=BF.
∴AE=BC,
又∵四边形ABCD为平行四边形,
∴AD=BC.
∴AE=AD.
∵CE=DC,
∴AC⊥ED,
∴四边形ABEC是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:数轴上有A、B、C三个点,它们表示的数分别是a、b和8,O是原点,且(a+20)2+|b+10|=0.
(1)填空:a= ,b= ;
(2)若将数轴折叠,使得点A与点C重合,则点B与数 表示的点重合;
(3)动点M在数轴上运动,是否存在点M使得MC+MB=20,若存在,请求出点M对应的数;若不存在,请说明理由;
(4)现有动点P、Q分别从A、B两点出发,点P以每秒3个单位长度的速度向点C移动,同时点Q以每秒1个单位长度的速度向点C移动.设点P移动的时间为t秒,问:
①当t为多少时,点P追上点Q?
②用含t的代数式表示线段PQ的长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节是我国的传统节日,人们有吃粽子的习惯.某校数学兴趣小组为了了解本校学生喜爱粽子的情况,随机抽取了50名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图(注:每一位同学在任何一种分类统计中只有一种选择)
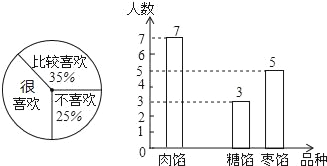
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”所对应的圆心角为 度;条形统计图中,喜欢“糖馅”粽子的人数为 人;
(2)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”粽子的人数之和;
(3)小军最爱吃肉馅粽子,小丽最爱吃糖馅粽子.某天小霞带了重量、外包装完全一样的肉馅、糖馅、枣馅、海鲜馅四种粽子各一只,让小军、小丽每人各选一只.请用树状图或列表法求小军、小丽两人中有且只有一人选中自己最爱吃的粽子的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:

(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①无理数都是无限小数;
②
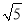 的算术平方根是3;
的算术平方根是3;③数轴上的点与实数一一对应;
④平方根与立方根等于它本身的数是0和1;
⑤若点A(﹣2,3)与点B关于x轴对称,则点B的坐标是(﹣2,﹣3).
其中正确的个数是( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.
A. ①③B. ②③C. ③④D. ②④
相关试题

