【题目】已知:数轴上有A、B、C三个点,它们表示的数分别是a、b和8,O是原点,且(a+20)2+|b+10|=0.
(1)填空:a= ,b= ;
(2)若将数轴折叠,使得点A与点C重合,则点B与数 表示的点重合;
(3)动点M在数轴上运动,是否存在点M使得MC+MB=20,若存在,请求出点M对应的数;若不存在,请说明理由;
(4)现有动点P、Q分别从A、B两点出发,点P以每秒3个单位长度的速度向点C移动,同时点Q以每秒1个单位长度的速度向点C移动.设点P移动的时间为t秒,问:
①当t为多少时,点P追上点Q?
②用含t的代数式表示线段PQ的长度?
参考答案:
【答案】(1)﹣20;﹣10;(2)﹣2;(3)存在点M使得MC+MB=20,点M对应的数为﹣11或9.(4)①当t为5时,点P追上点Q.②PQ=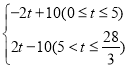 .
.
【解析】
(1)根据平方数的非负性、绝对值的非负性列出等式,求解即可;
(2)由折叠后重合的点表示的数之和不变,求解即可得;
(3)设点M对应的数为![]() ,分点M在点C的右侧(含点C)、点M在B、C两点之间(含点B)、点M在点B的左侧三种情形,根据
,分点M在点C的右侧(含点C)、点M在B、C两点之间(含点B)、点M在点B的左侧三种情形,根据![]() 列出等式求解即可;
列出等式求解即可;
(4)根据题意得,点P表示的数为![]() ,点Q表示的数为
,点Q表示的数为![]()
①点P追上点Q,则点P表示的数等于点Q表示的数,列出等式求解即可;
②由题①可知,点P追上点Q时,还未到达点C,所以分两种情况:在点P追上点Q之前、在点P追上点Q之后至到达点C,分别利用点P、Q代表的数作差即可.
(1)![]()
由平方数的非负性、绝对值的非负性得
![]() ,解得:
,解得:![]() ;
;
(2)由折叠后重合的点表示的数之和不变可得:![]()
故答案为:![]() ;
;
(3)设点M对应的数为![]() ,由题意分以下三种情形:
,由题意分以下三种情形:
①点M在点C的右侧(含点C),此时![]()
则![]() ,解得:
,解得:![]() ,符合
,符合![]() 的取值范围
的取值范围
②点M在B、C两点之间(含点B),此时![]()
则![]() ,方程无解
,方程无解
③点M在点B的左侧,此时![]()
则![]() ,解得:
,解得:![]() ,符合
,符合![]() 的取值范围
的取值范围
故存在这样的点M使得![]() ,点M对应的数为
,点M对应的数为![]() 或
或![]() ;
;
(4)由题意得,点P表示的数为![]() ,点Q表示的数为
,点Q表示的数为![]()
①点P追上点Q,则![]()
解得:![]()
答:当t为5时,点P追上点Q;
②由题意得,点P先追赶点Q,追上后会先到达点C
点P到达点C时,点P移动的时间![]() 为:
为:![]() ,即
,即![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
综上,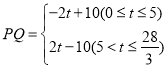 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一次,小明坐着轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,你能算出A点与湖中小岛M的距离吗?

-
科目: 来源: 题型:
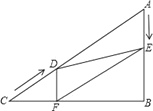
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节是我国的传统节日,人们有吃粽子的习惯.某校数学兴趣小组为了了解本校学生喜爱粽子的情况,随机抽取了50名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图(注:每一位同学在任何一种分类统计中只有一种选择)
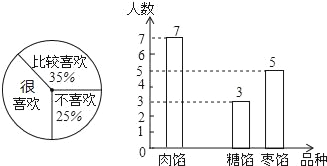
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”所对应的圆心角为 度;条形统计图中,喜欢“糖馅”粽子的人数为 人;
(2)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”粽子的人数之和;
(3)小军最爱吃肉馅粽子,小丽最爱吃糖馅粽子.某天小霞带了重量、外包装完全一样的肉馅、糖馅、枣馅、海鲜馅四种粽子各一只,让小军、小丽每人各选一只.请用树状图或列表法求小军、小丽两人中有且只有一人选中自己最爱吃的粽子的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:

(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
相关试题

