【题目】已知:如图,C为直线l上的一点,A、B为直线l外的两点,过A、B两点分别作直线l的垂线,垂足分别为点D、E,连接BC、AB,AB交直线l于点F,AC=BC,AD=CE.
求证:(1)CE=BE+DE;
(2)AC⊥BC.

参考答案:
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)由条件可证明Rt△ACD≌Rt△BCE,可得BE=CD,再利用线段的和差可证明CE=BE+DE;
(2)由(1)可得∠ACD=∠CBE,再结合Rt△CBE中,∠BCE+∠CBE=90°,可证得结论.
证明:(1)∵AD⊥l,BE⊥l,
∴∠ADC=∠CEB=90°,∠CAD=∠BCE,
∵AC=CB,AD=CE,
∴Rt△ADC≌Rt△CEB(HL),
∴CD=BE,
∵CE=CD+DE,
∴CE=BE+DE,
(2)由(1)可知Rt△ACD≌Rt△BCE,
∴∠ACD=∠CBE,
∵∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠BCE+∠ACD=90°,
∴∠ACB=90°,
∴AC⊥BC.
-
科目: 来源: 题型:
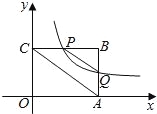
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线
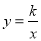 (x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)求k的取值范围;
(3)连接PQ,AC,判断:PQ∥AC是否总成立?并说明理由.
-
科目: 来源: 题型:
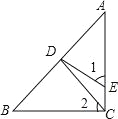
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
(1)若BC=3,AC=4,求CD的长;
(2)求证:∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中不正确的是( ).
A.-3.14既是负数,分数,也是有理数
B.0既不是正数,也不是负数,但是整数
C.-2000既是负数,也是整数,但不是有理数
D.0是非正数 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:①0是整数;②-3.5是负分数;③5.4不是正数;④自然数一定是正数;⑤负分数一定是负有理数,其中正确的有( ).
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=10cm,点C在直线AB上,如果BC=4cm,点D是线段AC的中点,求线段BD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人近期加强了锻炼,用“微信运动”记录下了一天的行走的步数为12400,将12400用科学记数法表示应为_____.
相关试题

